LoRA：low rank adaptation

• 用两个小矩阵相乘，去表示全量微调后权重矩阵的这个变化量

QLoRA（Quantized LoRA）详解

LoRA、QLoRA 讲解

通俗易懂理解全量微调和LoRA微调

摘要

1. 大语言模型应用重点：对通用领域数据进行大规模预训练，然后适应特定任务。（说人话就是先预训练一个能够处理通用任务的大模型，然后微调去适应特定领域）
2. 当模型越来越大时，全量微调变得不太可行。例如 GPT-3 有 175B 也就是1750亿个参数，代价高昂。
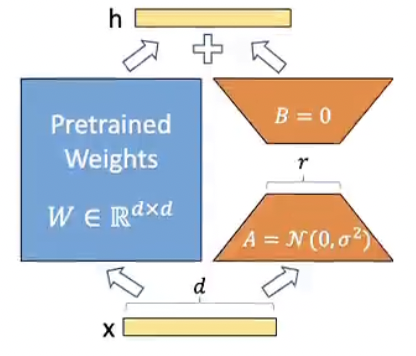
3. 提出低秩自适应，冻结预训练模型权重，不动原始参数，在旁边附加了一个结构：将一个可训练的秩分解矩阵注入到了 Transformer 架构每一层，大大减少下游任务训练所需参数量。
4. 一句话：用两个小矩阵相乘，去表示全量微调后权重矩阵的这个变化量。

方法

1. 矩阵的秩（Rank of a matrix）：指矩阵中线性无关的行或列的最大数量，反映矩阵包含的有效信息量。
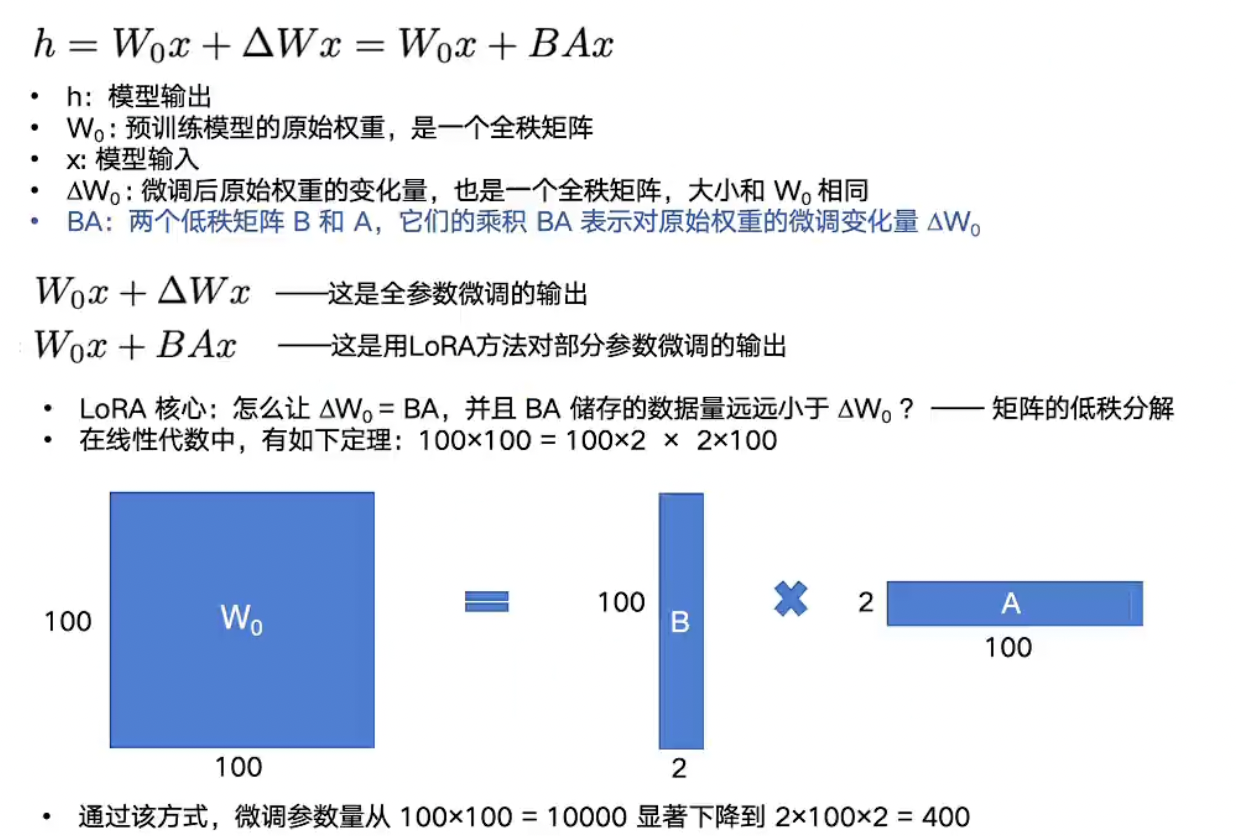
2. 表达式：h 是模型输出，x 是输入。前半部分是全参数微调输出的表达式，W0 是预训练模型原始权重，是一个非常大的满秩矩阵，delta_W0 是微调之后 W0 权重矩阵的变化量，也是一个全秩矩阵，大小和 W0 相同。
3. BA 是两个低秩矩阵 B 和 A，乘积表示了对原始权重矩阵微调的变化量 delta_W0。
4. LoRA 核心：怎么让 BA 去表示这个微调之后的权重变化量 delta_W0，并且让 BA 储存的数据量远小于这个巨大的全秩矩阵 delta。
5. 矩阵的低秩分解：线性代数中，矩阵乘法有如下原理，100 x 100 = 100x2 x 2x100（此处等号的意思是形状相同，并不指值等于）
6. LoRA 微调训练的是低秩矩阵，训练结束还需要进行权重合并。

Q：能不能直接训练一个由低秩分解矩阵构成的模型？

1. 低秩分解会限制模型的灵活性
   • 低秩分解的本质是减少参数量，但它也会限制矩阵的表达能力。
   • 对于复杂任务，原始权重矩阵需要保持高秩以捕获足够的信息。
   • 如果直接对其进行低秩分解，模型可能无法有效处理复杂的输入。

LoRA 相对于全量微调的优势

1. 不会有额外推理延迟：虽然引入了两个低秩矩阵，但可以通过将 BA 叠加到原始权重矩阵上，得到新的 W，直接用它让模型进行前向计算，计算过程和原来没区别，只是参数变了。
2. 如果要让模型适应另一个任务，要做的只是更新 BA。相当于提供一种很轻量的切换方式。

应用到 Transformer 架构中

1. 原文只针对自注意力模块的权重进行微调（Wq，Wk，Wv，Wo）
2. 实际应用也对 ffn 层对齐。
3. 适用于模型比较大的情况，如果模型本身比较小，或微调数据集比较小，建议用冻结部分参数，或全量微调。

实现

1. merge：最后使用这个线性层的时候，要不要把预训练的权重给用上去
2. rank：降到多少维
3. lora_alpha：权重以怎么样的比例缩放后和原始权重相加，如果训练出来权重太大，可能对原来干扰。（scale = lora_alpha / rank）
4. BA 初始化全 0，A 用 kaiming，B 用 zeros。B 是顶上那个。
5. linear 代表 W0，要 freeze 住。
6. 注意：之前一直有个误区，一个线性层 nn.Linear(in_features, out_features) 里面的矩阵大小 self.linear.weight 其实是 [out_features, in_features]，输入 x 大小为 [batch_size, in_features]。因为做的是 xWT，具体用 F.linear(input, self.weight, self.bias) 计算。
7. 因此 BA 矩阵的大小也应该是 [out_features, in_features]，和 W0 相同。

import torch
import torch.nn as nn
import torch.nn.functional as F

import math

class LoRALinear(nn.Module):
    def __init__(self, in_features, out_features, merge, rank=16, lora_alpha=16, dropout=0.5):
        super(LoRALinear, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.merge = merge
        self.rank = rank
        self.lora_alpha = lora_alpha
        self.dropout_rate = dropout
        # W0
        self.linear = nn.Linear(in_features, out_features)
        if rank > 0:
            self.Lora_b = nn.Parameter(torch.zeros(out_features, rank))
            self.Lora_a = nn.Parameter(torch.zeros(rank, in_features))
            self.scale = self.lora_alpha / self.rank
            self.linear.weight.requires_grad = False

        if self.dropout_rate > 0:
            self.dropout = nn.Dropout(self.dropout_rate)
        else:
            self.dropout = nn.Identity()

        self.initial_weights()

    def initial_weights(self):
        nn.init.kaiming_uniform_(self.Lora_a, a=math.sqrt(5))
        nn.init.zeros_(self.Lora_b)

    def forward(self, x):
        if self.rank > 0 and self.merge:
            # 合并后的新 W
            output = F.linear(x, self.linear.weight + self.Lora_b @ self.Lora_a * self.scale, self.linear.bias)
            output = self.dropout(output)
            return output
        else:
            output = self.linear(x)
            output = self.dropout(output)
            return output