Celeste

Celeste

Short biography for the left-hand sidebar

cs231n_cnn_1

7 minute read

Published:

CS231n_cnn: 1. Convolutional Neural Network

太长不看

  • 本节内容：卷积层，参数共享，池化层，全连接和卷积的转化，卷积网络的常见参数设置。
    1. 全连接架构在完整图像上是浪费的，大量参数将迅速导致过度拟合。
    2. 卷积网络明确假设输入是图像，神经元按三个维度排列：宽度，高度，深度（RGB）。每层把三维输入转化为三维输出。
    3. 神经元只和上层的一个小区域相连接，最终输出大小为 1x1x10，即输入图像在深度维度上，被压缩到代表类分数的单个向量。
    4. 维度的不同含义：
      1. 微观：输入个数。通过多少个维度来控制结果。
      1. 宏观：坐标轴个数（尺度）。需要从哪几个方向去描述物体的具体维度（这里的维度指：物体在不同轴上具体有多大）。
    • 输入有多少 dimensions：等同于有多少个输入(=size输入个数 [N, C, H, W])，也是所谓的 volume 体积，张量大小。high-dimensional inputs such as images, the volume has dimensions 32x32x3 (width, height, depth respectively)
    • 例如“可视化到二维平面”：就是用两个数描述平面上的一个点 [N, 2]
    • 和上述不同，卷积的3D volumes：卷积核大小的描述。三个方向输入的尺度，表示每个方向上有多少个点。layers of a ConvNet have neurons arranged in 3 dimensions: width, height, depth.
      1. 卷积网络由层堆叠而成，[INPUT - CONV - RELU - POOL - FC]。把图像三维输入转为类分数的三维输出。
      2. Conv层是卷积网络的核心，参数由一组可学习的滤波器组成，每个滤波器（卷积核）在宽度和高度上很小（感受野），但能覆盖输入的整个深度。例如，第一层的一个滤波器可能是[5x5x3]，前向传播过程中，沿输入的宽度和高度滑动，计算点积。滑过整个输入，每个滤波器都会得到一个二维的激活图，代表该滤波器在所有位置的反应。滑动时卷积核参数不变，即滑动过程共享参数。网络会学到某些特定滤波器，可以看到不同类型视觉特征，例如边缘、第一层的斑点，甚至是较高层上整体的轮廓。每个卷积层都有一组滤波器，例如12个，每个滤波器会输出一个二维激活图，沿深度维度堆叠这些激活图，得到输出。滤波器的个数就是输出的深度。
      3. 卷积核超参数：个数，感受野大小, stride, padding
    • 输出的深度：由滤波器的个数决定，每个滤波器关注不同特征。
    • 滤波器的滑动步长：1或2，步长越长输出的二维激活矩阵越小。
    • 在输入两侧补0：控制输出的大小，方便保持输出和输入宽高相同。
      1. 卷积的计算：输出大小 = (输入 - 卷积核 + 2 x padding) / 步长 + 1
    • 输入：W1 x H1 x D1
    • 4 个超参数：
      1. 滤波器个数 K
      2. 感受野 F
      3. 步长 S
      4. 补0数 P
    • 输出 W2 x H2 x D2
    • W2 = (W1 - F + 2*P) / S + 1
    • D2 = K
    • 每个滤波器参数个数：F * F * D1
    • 总参数：(F * F * D1) * K [weights]+ K [bias]
    • 通常设置 F = 3，S = 1，P = 1
      1. 参数共享：卷积核平移时不改变参数，总参数量为：滤波器个数*（3D卷积核大小+1）。平移不变性认为，提取例如边缘特征的卷积核，平移之后仍然有效。
      2. 卷积的并行计算，img2col（滑动窗口转化为并行的矩阵运算）：以AlexNet为例，输入[227x227x3]，96个卷积核11x11x3，步长4。得到输出激活图：55x55，也就是卷积核与输入图像平面计算的次数。卷积的过程可以看做：[55x55, 11x11x3] x [11x11x3, 96]。为什么1x1的卷积核也合理，因为卷积的对象是输入的整个depth。
      3. 池化：池化层夹在连续的卷积层中，通过MAX操作来减少参数和计算量，由此控制过拟合。最常见的滤波器大小为2x2，步长2，沿每一个深度层切片的宽高下采样一半，降到原先的四分之一，depth不变，不引入额外参数。
    • 输入：W1xH1xD1
    • 2个超参数：
      1. 空间范围 F
      2. stride S
    • 输出：W2xH2xD2
    • W2 = (W1 - F)/S + 1
    • D2 = D1
    • 通常只有两种设置：F = 3，S = 2 或 F = 2，S = 2.
      1. 一些网络去掉了池化，转而使用更大stride的卷积减少特征参数。抛弃池化层对于训练更好的生成网络很重要，例如VAEs，GANs。
      2. 全连接和卷积的相互转换：
        全连接和卷积层的唯一区别是：卷积核只和输入的局部相连，且平移中参数共享。但是由于计算方式都是点积，因此形式相同。
  • 全连接转卷积的思路：权重矩阵应当是很大且稀疏的，大部分都是0，除了特定block，因为要局部连接。由于参数共享，很多个block里的权重是相同的。优点在于，对于一个全都是卷积的网络，如果输入变大，原网络还可以用。
  • 用卷积当全连接的思路：就是把局部感受野扩大到整体，卷积核大小和输入相同。例如：输入是[7x7x512]，全连接输出 4096。用卷积：F=7,P=0,S=1,K=4096。这样输出为 1×1×4096。
    1. 卷积网络的结构：
      最常见的结构为：先堆几层 CONV-RELU，然后 POOL，这个block重复几次，在某个时候过渡到 FC-RELU，最后一层全连接输出到类分数。\

    INPUT -> [[CONV -> RELU]N -> POOL?]M -> [FC -> RELU]*K -> FC \

    N >= 0, 通常 N <= 3；M >= 0; K >= 0，通常 K < 3.\

    • INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC：池化层之间单卷积层。
    • INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]3 -> [FC -> RELU]2 -> FC：池化层之间有两个卷积层。对于更深更大的网络，这种做法很好，因为堆多个卷积层可以在具有破坏性的池化操作之前，提取更多复杂的输入特征。
      1. 堆叠多个小感受野滤波器，而不是只用一个大的，有更强的特征表达能力，和更少的参数量。
      2. 实践：基本不需要考虑模型架构问题，“don’t be a hero”：其实该做的是看看 ImageNet 上最有效的架构，然后下载一个预训练模型，在数据上微调。没必要从头开始设计和训练一个卷积网络。
      3. 卷积参数设置：
    • 输入：应当可以被多次除以 2。通常 32，64，96，224，384，512.
    • 卷积层：通常用小的 filters (例如 3x3 或 5x5)，stride = 1，用合适的 padding 使输入输出大小相等，例如 F=3，P=1；或 F=5，P=2。
    • 池化层：最常见的是 max-pooling，2x2 的感受野，stride = 2。丢掉 75% 的输入激活。
      1. 实践中更小的步长效果更好。特别的，步长为1，池化层负责全部下采样，而卷积层只需要把输入在 depth 维度上做变换。
      2. padding
    • 除了保持卷积层输入输出大小相同外，本质上为了提高性能。
    • 如果不用 zero-pad，每次经过卷积层，输入会越来越小，边缘部分的信息会被快速洗掉。

1. Architecture Overview

  1. 卷积神经网络和传统神经网络很像：都由神经元（可学习的权重和偏差），非线性组成，原始图像经过可微函数映射到类分数，用损失函数衡量好坏。
  2. 不同点在于卷积网络明确假设输入是图像，将这种明确特质编码到结构中，简化前向传播方程，减少参数量。
  3. 神经网络中，输入通过隐藏层转换，层与层间的神经元全连接，最后是输出层。
  4. 常规的神经网不能很好地扩展到完整图像。全连接结构在较大图像上的参数量是灾难级别，因为权重和输入维度相同，200x200x3 的图像有 120,000 个权重。全连接是浪费的，大量参数将迅速导致过度拟合。
  5. 三维神经元。由于卷积网络默认输入为图像，因此神经元也有三个维度：宽度，高度，深度（RGB）。例如输入图像为 32x32x3 (width, height, depth)。神经元只和前一层的一个小区域相连接，最终输出大小为 1x1x10，即输入图像在深度维度上，被压缩到代表类分数的单个向量。
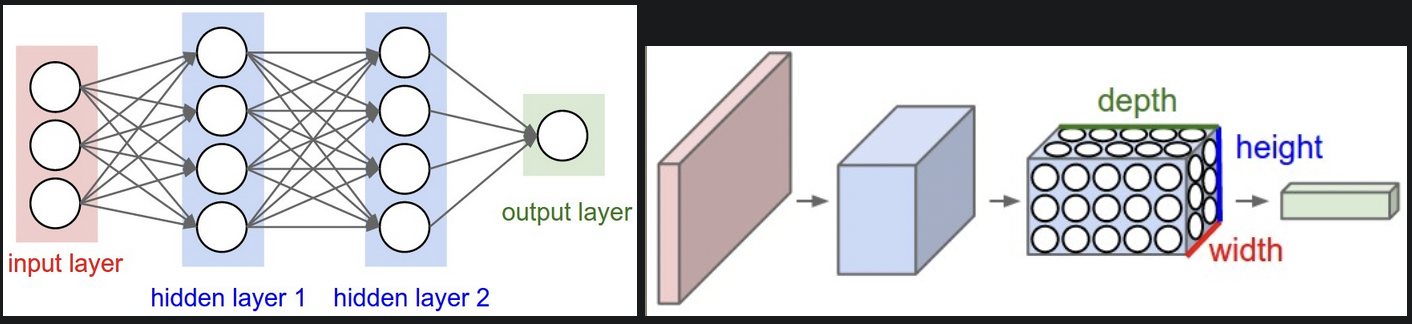
  • 左：三层的常规神经网络。
  • 右：卷积网络神经元按三个维度排列，每层把三维输入转化为三维输出。

2. Layers used to build ConvNets

  • 前言：卷积网络由层堆叠而成，主要有三种：卷积层，池化层，全连接。
  • 什么是卷积网络？层的序列，把图像三维输入转为类分数的三维输出。
  • 简单的CIFAR-10卷积网络架构：[INPUT - CONV - RELU - POOL - FC]
  • 输入 [32x32x3]
  • CONV: 接收三维输入，12个卷积核输出[32x32x12]
  • RELU: max(0, x) 输出 [32x32x12]
  • POOL: 下采样到 [16x16x12]
  • FC: 输出 [1x1x10]

把三维输入铺成一列

1. Convolutional Layer

  1. 概述：
    Conv层是卷积网络的核心，参数由一组可学习的滤波器组成，每个滤波器在宽度和高度上很小，但能覆盖输入的整个深度。例如，第一层的一个滤波器可能是[5x5x3]，前向传播过程中，沿输入的宽度和高度滑动，计算点积。滑过整个输入，每个滤波器都会得到一个二维的激活图，代表该滤波器在所有位置的反应。滑动时卷积核参数不变，即滑动过程共享参数。网络会学到某些特定滤波器，可以看到不同类型视觉特征，例如边缘、第一层的斑点，甚至是较高层上整体的轮廓。每个卷积层都有一组滤波器，例如12个，每个滤波器会输出一个二维激活图，沿深度维度堆叠这些激活图，得到输出。滤波器的个数就是输出的深度。

  2. Local Connectivity
    处理高维输入例如图像，不用全连接，而是只和输入的一部分关联。这个局部空间的大小是一个超参数，即感受野receptive field。卷积核在宽高的二维空间上有局部性，但在深度上总是和输入深度相同。
    例如：输入 size[32x32x3], receptive field[5x5], 卷积核权重为[5x5x3]，自动和输入深度对齐。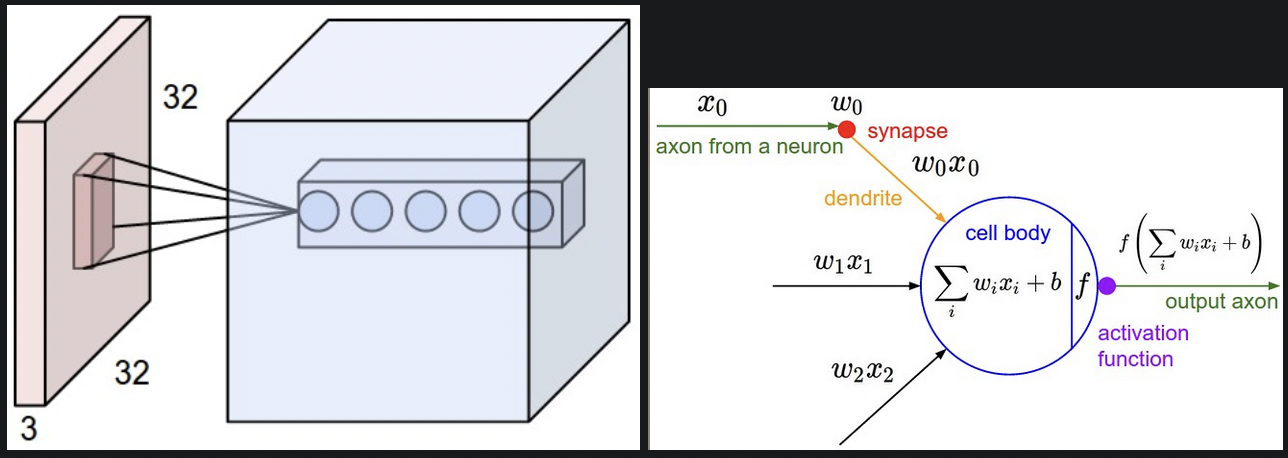

    红色部分为输入，5个卷积核，感受野都相同，但不共享参数。每个核深度为3。计算过程和传统神经网络相同，都是点积和非线性，区别在于局部空间。

  3. Spatial arrangement
    前面部分讨论了卷积核和输入图像的连接方式，下面讨论卷积核和输出的关系。三个超参数影响输出：depth, stride, padding
    • 输出的深度：由滤波器的个数决定，每个滤波器关注不同特征，例如边缘、颜色、斑点。这组神经元将输入的相同区域看作depth column。
    • 滤波器的滑动步长：1或2，每次移动跨过的像素数，步长越长二维输出越小。
    • 在输入两侧补0：控制输出的大小，方便保持输出和输入宽高相同。

    输出大小的计算公式：(输入 - 卷积核 + 2 x padding) / 步长 + 1

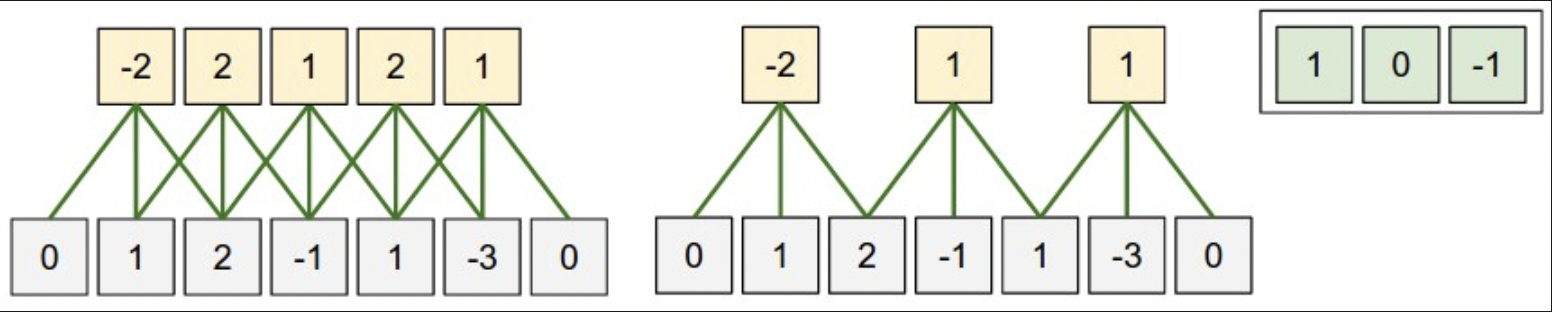
    单x轴可视化：一个感受野为3的卷积核[1, 0, -1]，输入大小为5，padding为1。

    • 左：步长为1，输出为(5 - 3 + 2)/1+1 = 5。注意：正是由于补了0，才让输出和输入的大小相同。
    • 右：步长为2，输出为(5 - 3 + 2)/2+1 = 3。
    • 步长限制：(W−F+2P)/S+1 一定得是整数，否则加padding，或crop输入图像。 AlexNet中：输入为[227x227x3]，第一个卷积层的神经元感受野为11，步长4，没有padding，卷积层深度为96。因此输出的神经元个数为555596，每个神经元都和输入的[11x11x3]大小区域相连。论文中提到输入图像大小为224x224，但代码实现不同，可能是用了3个像素的额外padding，但文中没提。
  4. Parameter Sharing
    如果这555596个神经元每个都有11113 = 363 weights and 1 bias，参数量就太大了。因此假设一个特征可以在点A处算出，那也可以在点B算出。即该卷积核在平移时不改变参数，参数量降到 961111*3。

    AlexNet中学到的96个卷积核可视化。每个滤波器大小为[11x11x3]。参数共享的假设相对合理：如果在图像某些地方检测边缘很重要，由于图像的平移不变性，这在其他位置也能用到。因此没必要每次55*55平移都重新学一个边缘特征的滤波器。

    • 有些情况下，参数共享的假设没意义。尤其输入图像有特定的中心结构，希望在图像另一边学到不同特征。例如输入为中心化的面部图像，希望在不同位置学到不同的眼部或头发特征。这种情况下叫局部连接层。
  5. Numpy examples
    # 某个点的 depth column：
X[x,y,:]
# 某一层的整个激活图：
X[:,:,d]

# 输入X.shape: (11, 11, 4), padding=0, filter_size=5, stride=2，则output_size(特征激活图大小) = (11 - 5) / 2 + 1 = 4，卷积过程:
V[0, 0, 0] = np.sum(X[:5, :5, :] * W0) + b0
V[1, 0, 0] = np.sum(X[2:7, :5, :] * W0) + b0
V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0

v[0, 1, 1] = np.sum(X[:5, 2:7, :] * W1) + b1
   
# W0.shape: (5, 5, 4)
  6. Conv Layer Summary
    • 输入：W1 x H1 x D1
    • 4 个超参数：
      1. 滤波器个数 K
      2. 感受野 F
      3. 步长 S
      4. 补0数 P
    • 输出 W2 x H2 x D2
    • W2 = (W1 - F + 2*P) / S + 1
    • D2 = K
    • 每个滤波器参数个数：F * F * D1
    • 总参数：(F * F * D1) * K [weights]+ K [bias]
    • 通常设置 F = 3，S = 1，P = 1

  7. Convolution Demo
    把3D按深度平铺了，输入volume：W1 = 5, H1 = 5, D1 = 3，卷积层：K = 2, F = 3, S = 2, P = 1。即有两个3x3的卷积核，步长2。由此计算输出激活图大小为 (5 - 3 + 2) / 2 + 1 = 3.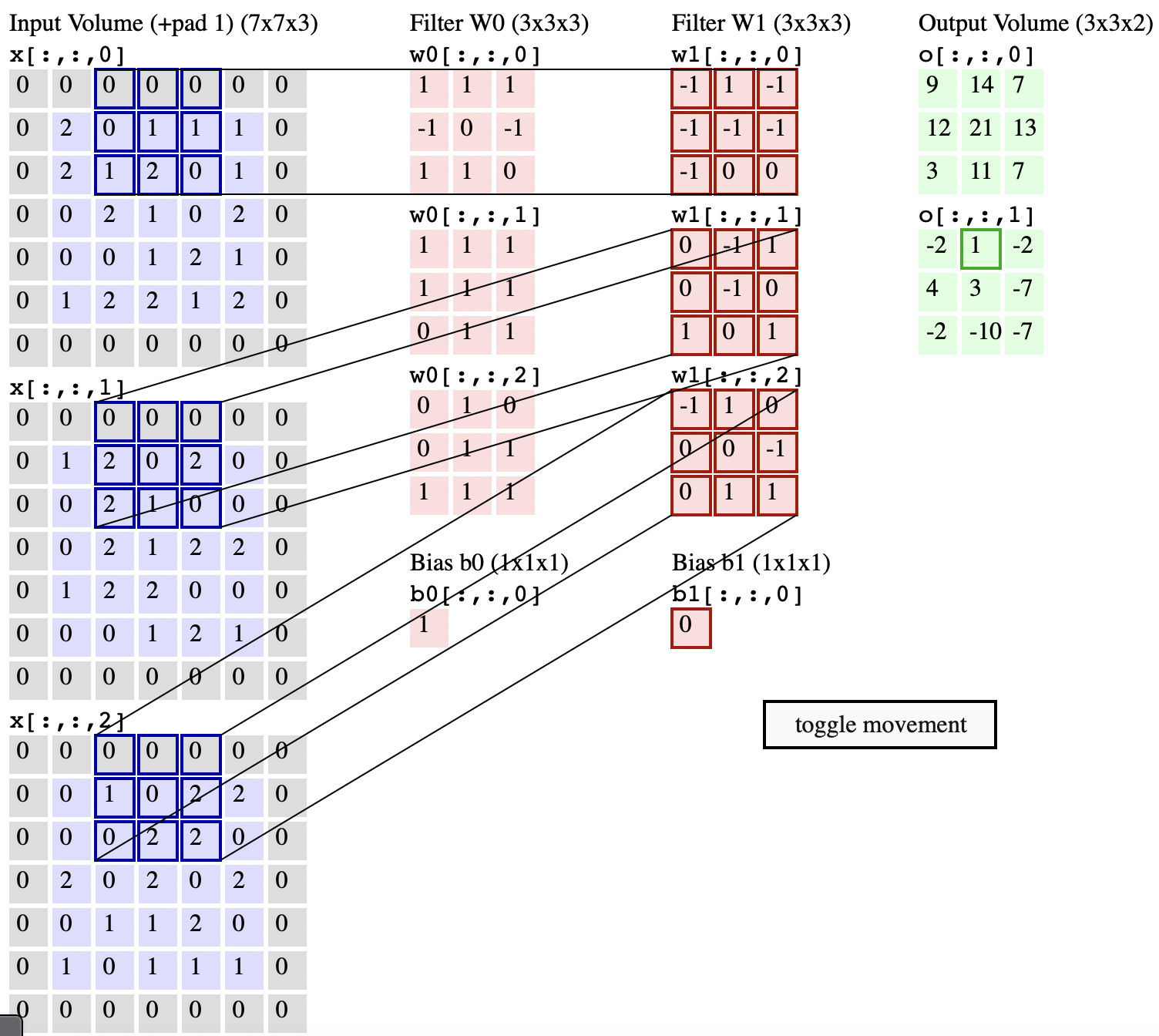

  8. Implementation as Matrix Multiplication
    • 卷积操作的本质是卷积核和局部输入做点积。
    • 怎样转化成矩阵运算呢？其实就是[感受野 x 个数]。把感受野那部分拉直，看成列向量。
    • 例如AlexNet的设置，输入[227x227x3]，96个卷积核11x11x3，步长4。输出大小即为单轴上的计算次数：(227-11)/4+1 = 55。得到输入转矩阵：im2col[11x11x3, 55x55] = [363 x 3025]
    • 同理对于卷积层转矩阵：[96, 11x11x3]，把感受野拉直成行向量，意为有多少个大小为这么大的卷积核。
    • 矩阵运算：np.dot(W_row, X_col)，每个滤波器和每个感受野位置做点积。得到[96x3025]，再按宽高深reshape成[55x55x96]输出。
    • 矩阵运算的缺点是会耗费大量内存，因为卷积有重叠区域，存在重复计算。优点是实现简单。

  9. Backpropagation
    卷积操作的反向传播也是卷积，只是卷积核翻转下。

  10. 1x1 convolution
    为什么1x1的卷积核也合理，因为卷积的对象是输入的整个depth。例如输入图像为[32x32x3]，1x1的卷积也是做的3个维度上的点积。

  11. Dilated convolutions
    在Conv层多引入一个超参：间隔。使感受野不是连续的，例如：dilation=1，w[0]x[0] + w[1]x[2] + w[2]*x[4]。间隔卷积和连续卷积联合使用，可以叠更少的卷积层，就看完整个图。

2. Pooling Layer

  1. 概述
    池化层夹在连续的卷积层中，通过MAX操作来减少参数和计算量，由此控制过拟合。最常见的滤波器大小为2x2，步长2，沿每一个深度层切片的宽高下采样一半，降到原先的四分之一，depth不变，不引入额外参数。
    • 输入：W1xH1xD1
    • 2个超参数：
      1. 空间范围 F
      2. stride S
    • 输出：W2xH2xD2
    • W2 = (W1 - F)/S + 1
    • D2 = D1
    • 通常只有两种设置：F = 3，S = 2 或 F = 2，S = 2.

  2. General Pooling
    池化操作除了 MAX 还可以 average pooling 或 L2-norm pooling。实践通常用 MAX，也是最常用的下采样操作，因为效果更好。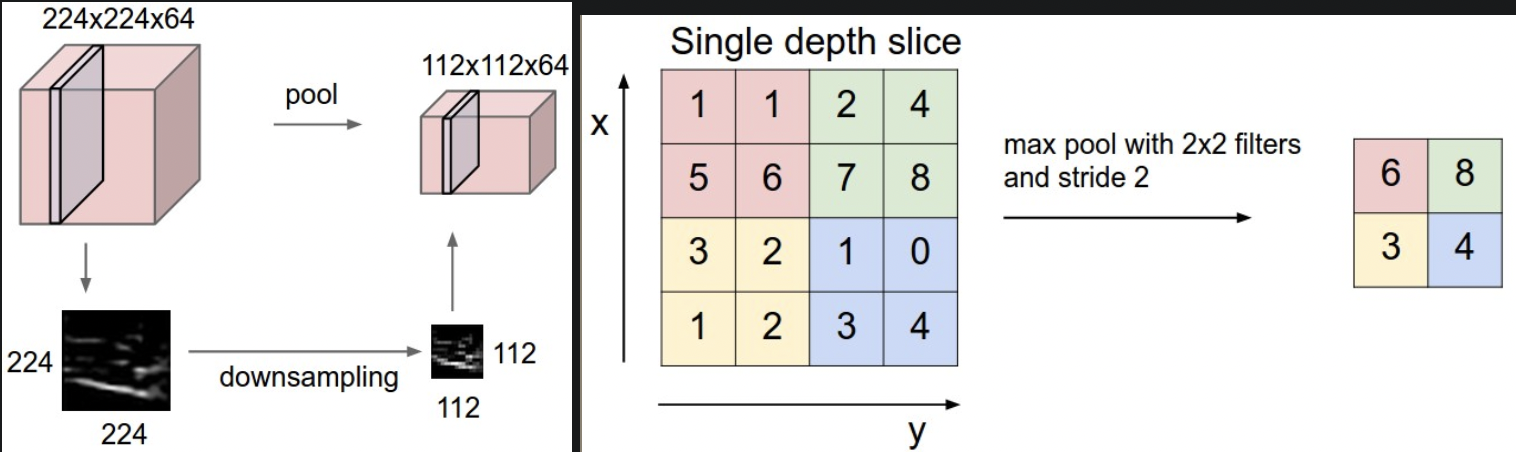

    对depth上的每个切片执行下采样。F=2，S=2。max 是最常用的下采样操作。

  3. Backpropagation
    max操作对最大的输入值才有梯度，因此在前向传播中跟踪最大的激活值。

  4. Getting rid of pooling
    一些网络去掉了池化，转而使用更大stride的卷积减少特征参数。抛弃池化层对于训练更好的生成网络很重要，例如VAEs，GANs。可能在未来架构里池化层很少。

3. Normalization Layer

过去提出了多种归一化层，但影响很小。详见：Alex Krizhevsky’s cuda-convnet library API.

4.Fully connected layer

全连接和常规神经网络中相同。

5. Converting FC layers to CONV layers

全连接和卷积层的唯一区别是：卷积核只和输入的局部相连，且平移中参数共享。但是由于计算方式都是点积，因此形式相同。

  • 全连接转卷积的思路：权重矩阵应当是很大且稀疏的，大部分都是0，除了特定block，因为要局部连接。由于参数共享，很多个block里的权重是相同的。
  • 用卷积当全连接的思路：就是把局部感受野扩大到整体，卷积核大小和输入相同。例如：输入是[7x7x512]，全连接输出 4096。用卷积：F=7,P=0,S=1,K=4096。这样输出为 1×1×4096。
  1. FC->CONV conversion
    把全连接层转化为卷积层在实践中很有用。例如：对于224x224x3的输入，经过一系列卷积和池化层，缩小到7x7x512的激活。AlexNet中，用5个池化层完成，即 224/2^5=7。然后用了三层全连接：两个4096，最后1000。把这三层全连接转成卷积：
    • 第一层：卷积核 [7x7x512]，4096个。
    • 第二层：卷积核 F=1，4096个。
    • 第三层：F=1，1000个。 考虑一个场景：输入图像变大了，但还想用原来的网络处理，这时因为全连接和输入大小有关，就要把输入作crop，分多次输入网络。但如果用fc转换成的卷积一次就能跑通。（为什么不直接resize呢？是不想丢失信息吗）
      例如：对于一个将224x224输入图像降32到[7x7x512]输出的卷积网络，用更大的输入图像384x384，得到输出[12x12x512]。这时，如果原始网络用的是全连接就跑不了，但是用卷积就能输出[6x6x1000]，得到6x6的类分数矩阵。
      Evaluating the original ConvNet (with FC layers) independently across 224x224 crops of the 384x384 image in strides of 32 pixels gives an identical result to forwarding the converted ConvNet one time. 意思是与其用32的步长裁剪36次，还不如用转换过的卷积直接跑，得到36个类分数。
      实践中：通常把图像resize成更大，然后用这种经过转换的卷积网络，得到多个空间位置的类分数，最终取均值 to get better performance。
      如果步长小于32呢？（为什么一定是32，可能因为AlexNet把原始图像在宽高上缩了32）跑多次：假如步长16，先用原始图像跑一次，再用在宽高上都移动了16个像素的图像跑。

2. ConvNet Architectures

概述：CONV，RELU, POOL, FC 这些最常见的组件如何组成卷积网络。

1. Layer Patterns

  1. 概述
    最常见的结构为：先堆几层 CONV-RELU，然后 POOL，这个block重复几次，在某个时候过渡到 FC-RELU，最后一层全连接输出到类分数。\

    INPUT -> [[CONV -> RELU]N -> POOL?]M -> [FC -> RELU]*K -> FC \

    N >= 0, 通常 N <= 3；M >= 0; K >= 0，通常 K < 3.\

    • INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC：池化层之间单卷积层。
    • INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]3 -> [FC -> RELU]2 -> FC：池化层之间有两个卷积层。对于更深更大的网络，这种做法很好，因为堆多个卷积层可以在具有破坏性的池化操作之前，提取更多复杂的输入特征。

  2. 用多个小滤波器叠加，而非用一个有大感受野的
    比如有三个3x3的滤波，每层之间有非线性。第二层卷积能看到输入的5 x5，第三层能看到输入的7x7。比起只用一个7x7的卷积，首先更多的非线性，意味着更强的特征表现能力；其次参数量更少。假如输入和卷积核的channel都是C，则7x7为C×(7×7×C)，三个3x3为3×(C×(3×3×C))。
    总结：堆叠多个小感受野滤波器，而不是只用一个大的，有更强的特征表达能力，和更少的参数量。

  3. Recent departures
    • Google’s Inception
    • Residual
  4. In practice：use whatever works best on ImageNet
    基本不需要考虑模型架构问题，“don’t be a hero”：其实该做的是看看 ImageNet 上最有效的架构，然后下载一个预训练模型，在数据上微调。没必要从头开始设计和训练一个卷积网络。

2. Layer Sizing Patterns

本节介绍卷积网络每层通常的超参数设置。首先说明对架构进行调整的常见经验：

  1. Input layer
    输入应当可以被多次除以 2。通常：32 (CIFAR-10), 64, 96 (eSTL-10), or 224 (common ImageNet ConvNets), 384, and 512.

  2. Conv layer
    • 通常用小的 filters (例如 3x3 或 5x5)，stride = 1，用合适的 padding 使输入输出大小相等，例如 F=3，P=1；或 F=5，P=2。
    • 总结一下就是：P=(F−1)/2 的情况可以保留输入大小。
    • 如果必须用很大的 filter，通常只用在第一层，直接看输入图像。
  3. Pool layer
    • 主要负责对输入的空间维度下采样。
    • 最常见的是 max-pooling，2x2 的感受野，stride = 2。丢掉 75% 的输入激活。
    • 不太常见的是 3x3 receptive field，S = 2。这种可能要padding。感受野基本不超过 3.

  4. Reducing sizing headaches
    上述方案的卷积层都保留了输入大小，因此只有池化层负责下采样。还有其他方案，例如 Conv stride > 1，或者不用 padding。此时卷积输出大小和输入不等。

  5. Why use stride of 1 in CONV?
    实践中更小的步长效果更好。特别的，步长为1，池化层负责全部下采样，而卷积层只需要把输入在 depth 维度上做变换。

  6. Why use padding?
    • 除了保持卷积层输入输出大小相同外，本质上为了提高性能。
    • 如果不用 zero-pad，每次经过卷积层，输入会越来越小，边缘部分的信息会被快速洗掉。the information at the borders would be “washed away” too quickly.
  7. 基于内存连续性的妥协
    早期模型由于GPU内存瓶颈，实践中倾向于在网络第一个卷积层，用较大的 filter size 和 stride 得到较小的激活图（如果保持输入输出大小相同，内存放不下）。例如 AlexNet 的 F=11x11，S=4.

3. Case studies

  1. LeNet
    第一个成功的卷积网络。Yann LeCun in 1990’s. was used to read zip codes, digits, etc.

  2. AlexNet
    ILSVRC 2012，第一个知名的计算机视觉卷积网络。和 LeNet 架构相似，但更深，更大，并且堆叠了连续的卷积层。（过去通常只用一层卷积，后面就紧跟着池化了）

  3. ZF Net
    ILSVRC 2013，改进了 AlexNet 架构的超参数，特别是扩大了中间卷积层的大小，减小第一层的 stride 和 filter size。

  4. GoogLeNet
    ILSVRC 2014，主要贡献是 Inception Module，极大减小了网络参数(4M, compared to AlexNet with 60M)。此外，用了平均池化代替全连接，去掉了很多不重要的参数。衍生出了 Inception 系列。

  5. VGGNet
    ILSVRC 2014 亚军，主要贡献是表明了网络的深度对性能有关键影响。网络最终架构有 16 个卷积和全连接层，只用了3x3卷积和2x2下采样，极其对称。缺点是参数多(140M)，大部分参数集中在第一个全连接层，且去掉这些全连接层对性能也没影响。

  6. ResNet
    ILSVRC 2015，用了特殊的 skip connection 和大量的 batch normalization。且网络的最后也没用全连接。实践中最常用的架构。

  7. VGGNet in detail \

    • Conv layers：3x3，stride=1，pad=1
    • Pool layers：2x2，stride=2
INPUT: [224x224x3]        memory:  224*224*3=150K   weights: 0
CONV3-64: [224x224x64]  memory:  224*224*64=3.2M   weights: (3*3*3)*64 = 1,728
CONV3-64: [224x224x64]  memory:  224*224*64=3.2M   weights: (3*3*64)*64 = 36,864
POOL2: [112x112x64]  memory:  112*112*64=800K   weights: 0
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*64)*128 = 73,728
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*128)*128 = 147,456
POOL2: [56x56x128]  memory:  56*56*128=400K   weights: 0
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*128)*256 = 294,912
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
POOL2: [28x28x256]  memory:  28*28*256=200K   weights: 0
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*256)*512 = 1,179,648
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
POOL2: [14x14x512]  memory:  14*14*512=100K   weights: 0
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
POOL2: [7x7x512]  memory:  7*7*512=25K  weights: 0
FC: [1x1x4096]  memory:  4096  weights: 7*7*512*4096 = 102,760,448
FC: [1x1x4096]  memory:  4096  weights: 4096*4096 = 16,777,216
FC: [1x1x1000]  memory:  1000 weights: 4096*1000 = 4,096,000

TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd)
TOTAL params: 138M parameters

可以看到，大部分显存用在前面的卷积层，而大部分参数集中在全连接层，特别是第一个全连接，有 100M 权重，同时整个网络参数量为 140M。

4. Computational Considerations

构建卷积架构时最大的瓶颈是存储，现在GPU很多8G，12G显存。存储占大头的主要是：

  • intermediate volume sizes：这些是卷积网络每层的原始激活，同时也是梯度大小。通常大多数激活都位于第一个卷积层，存着用于反向传播。
  • parameter sizes：包括网络参数，反向传播时的梯度，和优化过程的cache。
  • miscellaneous memory：例如 image data batches，和 augmentation。

大致估计后，转为GB：先乘 4 得到 字节数，然后除以三次 1024，得到 KB，MB，GB。如果显存装不下模型，通常减小 batch size，因为输入激活占了大部分存储。

You May Also Enjoy

[llms] 笔记文档

6 minute read

Published:

（该页面的 .md 和 .pdf 文件已放在视频简介，.md 文件可用该软件 (Obsidian) 或用 VS Code打开）

一、简介

本期视频主要分为以下五部分：

1. 需求和技术
  • 企业对于大模型的不同类型个性化需求
  • SFT（有监督微调）、RLHF（强化学习）、RAG（检索增强生成） -关注：基本概念；分别解决什么问题；如何根据需求选择；
  • 微调部分详细介绍：
    • 微调算法的分类
    • **LoRA 微调算法
    • 微调常见实现框架
      2. 整体步骤说明
  • 在 Linux 系统上微调一个大模型、部署模型、暴露 API 给 web 后端调用，本机前端展示全过程
    3. 模型微调
  • 框架: LLama-Factory (国产最热门的微调框架)
  • 算法: **LoRA (最著名的部分参数微调算法）
  • 基座模型：DeepSeek-R1-Distill-Qwen-1.5B -蒸馏技术通常用于通过将大模型（教师模型）的知识转移到小模型（学生模型）中，使得小模型能够在尽量保持性能的同时，显著减少模型的参数量和计算需求。
    4. 模型部署和暴露接口
  • 框架：FastAPI（一个基于 python 的 web 框架）
    5. web后端调用
  • 通过 HTTP 请求交互即可（ Demo 前后端代码都在视频简介）

[llms] Docs

less than 1 minute read

Published:

个人向学习文档

采样

1 minute read

Published:

sample

  • 采样目的：生成文本时，从预测结果中选出高概率的候选词，避免随机选到低概率词导致的语句不合理，同时保留一定多样性。
  • 先用temperature 调整分布平滑度，然后 top-k + top-p 控制候选范围

MoE 原理及实现

less than 1 minute read

Published:

MoE：mix of experts

  • 专家 stack 起来，计算 token 经过每个专家的输出，对结果加权。