cs231n_7
Published:
CS231n: 7. Learning the parameters
太长不看
- 本节内容:网络训练部分。包括训练前的梯度检查、健壮性检查;训练时要监控的指标;参数更新方式;学习率衰减;随机搜索超参数;模型集成。
- 网络训练之前,健壮性检查:确保使用小参数进行初始化时得到预期损失。先只用数据损失,初始化每个类的概率应相同,算loss:-ln(0.1) = 2.302。然后加上正则项,总损失应当增加。
- 先确保能过拟合一小部分训练数据。参数:权重+偏差
- 训练时,监控指标:loss,acc。用于调超参数。x 轴是 epoch,表示每个样本在训练中被看过的次数。
- loss 形状反映了学习率。
- 学习率小:loss 线性下降。
- 学习率增大:loss 指数下降。
- 较大的学习率:loss 降的更快,但会卡在较差的值。因为动能太大了,参数乱跳,无法安定在最优位置。
- loss 的震荡和 batch size 有关,bs越小震荡幅度越大。
- 训练集和验证集 acc 的差距表明了过拟合程度。
- 差距过大,严重过拟合,通过增强正则化:加大 L2 惩罚,更多 dropout。或增加数据量。
- 紧密贴合,模型容量不足,增加参数量,让模型变大。
- 错误初始化会减慢甚至停止学习过程。绘制所有层的激活/梯度直方图,观察输出分布。例如 tanh,希望分布在[-1,1],而不是全输出 0,或集中在两端。
- 反向传播算梯度,梯度是权重的多维导数,决定了权重更新的方向,即 loss 下降的方向,用于更新参数。损失函数空间是多维的,可能从初始点出发,前后摇摆到最低鞍点,此时应当还有部分动能,支持该点继续向左右移动直达最小值。
- 传统参数更新,对所有权重一视同仁:SGD,SGD momentim。
- SGD:权重改变量 = 步长(学习率) * 方向(梯度)
- SGDM:引入摩擦力,在学习后期会增加,来降低系统动能。
- 上述学习率为定值,但实践中,我们希望全局学习率衰减。常用按 epoch 衰减,先用固定学习率训练,看验证集 loss,当损失不降时,将学习率减半。选择较慢的衰减,训练时间长点。
- 自适应学习率,根据具体参数的梯度(注意,全局学习率不会因此改变):Adagrad,RMSprop,Adam
- Adagrad:梯度大的权重,学习率会小,更新不那么频繁的权重学习率会提高。缺点:学习率单调递减,会过早停止学习。
- RMSprop:解决单调问题,引入额外超参 decay_rate
- Adam:引入动量(摩擦力),对原始梯度平滑处理。eps = 1e-8, beta1 = 0.9, beta2 = 0.999
- 虽然个体学习率会自适应,并不意味着全局学习率不用衰减。
- 鞍点:SGD 很难打破对称性并卡在顶部。相反,RMSprop 等算法会在鞍座方向看到非常低的梯度。由于 RMSprop 更新中的分母项,这将增加沿该方向的有效学习率,帮助 RMSProp 继续进行。
- 超参数:
- 初始学习率
- 学习率衰减 schedule(衰减常数值)
- 正则强度(L2 penalty, dropout 强度)
- 超参数搜索的实现:
- worker:持续随机采样超参数,执行优化。在训练期间,worker 记录每个 epoch 验证集的表现,将 model checkpoint 写入文件,文件名为验证集表现。
- master:在计算集群中启动或终止 worker,并检查 checkpoint,绘制训练数据。
- 很多人说交叉验证了一个参数,实际上只用了单个验证集。
- 随机搜索:
- 以 10 为底数,从均匀分布中随机采样,例如:learning_rate = 10 ^uniform(-6, 1) \
- dropout = uniform(0,1) \
- 最后记得检查下区间端点的取值。
- 搜索实践: 先在大概范围内搜索,然后根据最佳结果的取值,缩小搜索范围。\
- 在第一个 epoch 内进行初始的粗粒度搜索,因为很多不正确的超参数设置会导致模型不学习,或loss爆炸。 \
- 第二阶段可以用 5 个 epoch 进行小范围搜索。 \
- 第三阶段用更多 epoch,在最终确定的小范围内进行详细搜索。
- 构建集成:
- Running average of parameters during training.
一种低成本提升1-2个点性能的方式:把网络权重copy下来,其中包含训练时权重的指数衰减记录。取最后几个迭代,求权重的均值。这个平滑版本的集成权重在验证集的性能往往会更好,因为直觉上目标函数是碗状的,模型在曲线上来回跳,取最后几步的均值有更高的概率接近最低点。 - 新的思想是通过合并集成的 log likelihods 到一个修改后的目标,将集成”蒸馏”回单个模型。
阶段总结
- 线性分类器:y = Wx + b,10个类
图像输入 x 为 [224 x 224 x 3, 1] 的列向量,W 为 [10, 224x224x3] 的矩阵,其中每一行是一个类的分类器。
文本输入时,x 为 [N, seq_len],一句话先被截为定长,不够就补0,保证batch内padding到一样长就行。按字典做one-hot,然后词嵌入到语义空间。[N, seq_len, d_model]。输入的 seq_len 可变长,因为模型处理的是 d_model - 线性分类器实现时,W 为 [class_num, D],输入 x 为 [N, D],计算矩阵乘法 xW_T
文本输入时,Transformer 多头注意力中 W_k 大小为 [d_k, d_model],和 embedding 后的输入 x: [batch_size, seq_len, d_model] 计算矩阵乘法 xW_T = [batch_size, seq_len, d_k]。 - 从0-1高斯分布中随机初始化 W 的参数,取第一个batch的数据,更新一次参数。更新过程为先算最终loss,然后反向传播,算每个参数的梯度,用SGDM或Adam的方式更新参数。看完一个batch的数据就更新一次参数,算一次loss。这个过程可视化为一个球在loss空间中来回滚动,W矩阵的数字在不断跳动,小球要到达山坡最低点。本质上就是凸函数优化:不断求导,明确方向,逐渐逼近极值。
- 扩展到神经网络,s = W_2 max(0, W_1x),W1 是 [100, 3072],将图像转换为 100 维中间向量。max(0,−) 是非线性函数,将所有小于 0 的激活 阈值设置为 0. 最后用 W2 [10, 100] 转回 10 类分数。相当于两个线性层中加了非线性激活函数。
- 模型往大了选,用正则化和dropout处理过拟合。过拟合:模型拟合能力过强,导致高度拟合了噪声数据。大网络局部最优多,但每个局部最小值 loss 小,总体 loss 方差小,不依赖初始化。
- 数据划分:先分好训练和测试,然后训练数据分成训练集和验证集,5折交叉验证。原则:先划分再处理。
- 数据预处理:先0中心化,即减去均值。然后归一化:缩放到[-1, 1]。均值要在训练集上计算,然后应用于验证集和测试集。还可以做PCA降维。
- 模型设置:
- 权重初始化:w = np.random.randn(n) * sqrt(2.0/n) 从均值 0 方差 1 的高斯分布随机采样,然后用方差归一化。
- 激活函数:ReLU
- BatchNorm:在全连接层后,非线性层前。可以看做是在网络每一层进行预处理。
- L2 regularization (weight_decay): 对权重平方惩罚。分散,小权重。
- Dropout:训练时对网络随机采样,仅更新子网络部分的参数。测试时,计算所有子网络集成的平均。
- 模型检查:先确保能过拟合一小部分训练数据。
- 训练时:
- 监控 loss,acc。
loss 反映学习率,震荡反应batch_size,acc 反映过拟合程度,过拟合加强正则和dropout,欠拟合增大模型容量。 - 学习率衰减:常按 epoch 衰减,先用固定学习率训练,看验证集 loss,不降时,将学习率减半。选择较慢的衰减,训练时间长点。或每5个epoch减半,每20个乘0.1。
- SGDM:随机梯度下降的基础上引入摩擦力,训练后期降低系统动能,让小球停下。
- Adam:针对具体参数的梯度自适应学习率,鞍点学不下去快停的时候推一把。梯度大的权重,学习率会小,更新不频繁的权重学习率会提高。学习率递减不单调,对原始梯度平滑处理。eps = 1e-8, beta1 = 0.9, beta2 = 0.999
- 监控 loss,acc。
- 模型超参数:
- 初始学习率
- 学习率衰减 schedule
- 正则强度(L2, dropout)
- 超参数随机搜索:以 10 为底数,从均匀分布中随机采样,例如:learning_rate = 10 ^uniform(-6, 1)
- worker:在训练期间记录每个 epoch 验证集的表现,将 model checkpoint 写入文件,文件命名为valid_acc。
- master:控制 worker,检查 checkpoint,绘制训练数据。
- 很多人说交叉验证了一个参数,实际上只用了单个验证集。
1. Gradient Checks
comparing the analytic gradient to the numerical gradient
- Use the centered formula.
- Use relative error for the comparison.
- Use double precision.
- Stick around active range of floating point.
- Kinks in the objective. 指目标函数的不可微部分,例如 ReLU,SVM 引入的 max 操作。
- Use only few datapoints.
- Be careful with the step size h.
学习率不是越小越好,通常 1e-4,1e-6 - Gradcheck during a “characteristic” mode of operation.
梯度检查是在参数空间中特定的单点上执行,不是全局。为了安全起见,最好使用较短的老化时间,在此期间允许网络在损失开始下降后学习并执行梯度检查。 - Don’t let the regularization overwhelm the data.
如果 正则化loss 盖过了 data loss,梯度主要来自正则化,可能掩盖 data loss 的错误。一般先不要正则项,确定 data loss 正确,然后再加。 - Remember to turn off dropout/augmentations. \
- Check only few dimensions.
2. Before learning: sanity checks Tips/Tricks
- 参数初始化后,检查一下数据损失的初始值.
- 10 类,Softmax 初始化 loss = -ln(p=0.1) = 2.302
- SVM loss = 9
- 然后加上正则化,损失应当增加。
- 过拟合一小部分数据。
在对完整数据集进行训练之前,尝试对数据的一小部分(例如 20 个示例)进行训练,并确保可以实现 0 loss。(无正则)
注意,如果这小部分数据有问题,在完整数据集上不会泛化。
3. Babysitting the learning process
- x 轴单位是 epoch,一个 epoch 意味每个样本都被看过一次。最好不用 iterations,因为和 batch size 有关。一个 batch 更新一次。
- Loss function
每个 batch 更新一次参数,算一次 loss,最终整个 epoch 求和的均值。
loss 的形状反映了学习率。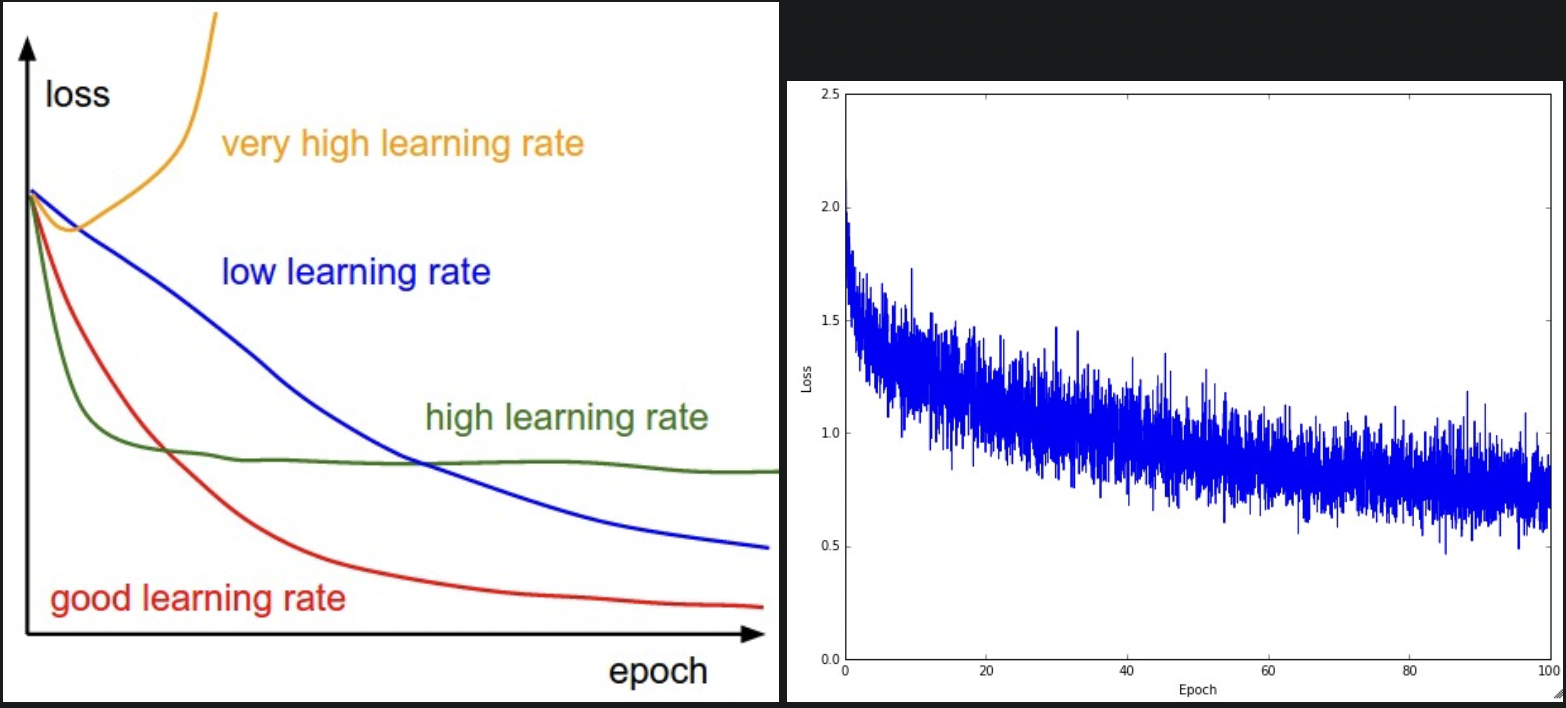
- 学习率小:loss 线性下降。
- 学习率增大:loss 指数下降。
- 较大的学习率:loss 降的更快,但会卡在较差的值。因为动能太大了,参数乱跳,无法安定在最优位置。
- 右图:看似合理的学习率,(但衰减速度有点慢,可能学习率小了,且 batch size 小了,因为噪声较多,震荡较大。)\
loss 的震荡和 batch size 有关,越小震荡幅度越大,当 batch size 是整个数据集时,理论最小,因为每次梯度更新对 loss 的影响应该是单调的。\
把交叉验证的 loss 放一张图里对比。
- Train/Val accuracy
准确率反应了过拟合情况。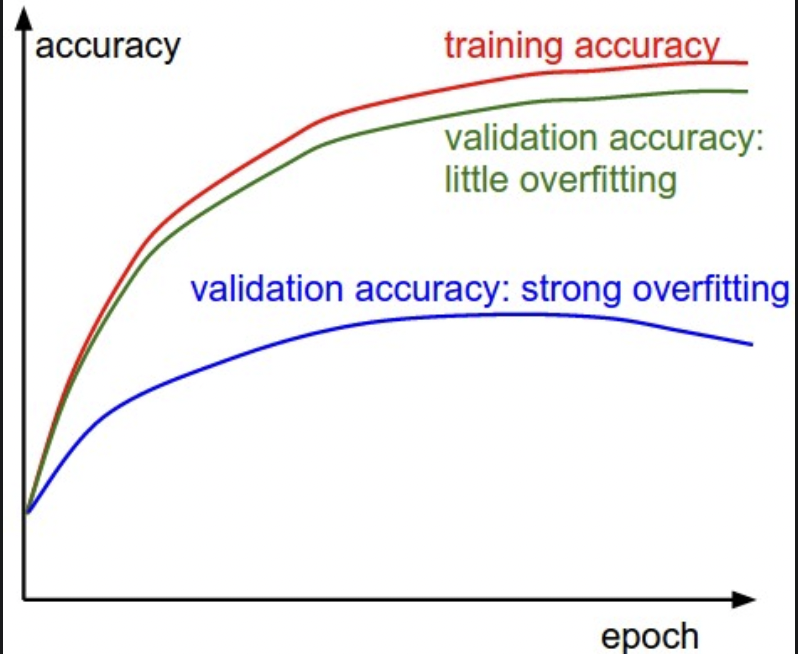
- 训练集和验证集 acc 的差距表明了过拟合程度。
- 蓝:差距过大,严重过拟合,通过增强正则化:加大 L2 惩罚,更多 dropout。或增加数据量。
- 绿:紧密贴合,模型容量不足,增加参数量,让模型变大。
- Ratio of weights:updates
参数 更新的幅度 和 大小 的比例:学习率 * 参数梯度 / 参数大小。一般是 1e-3,反应学习率大小。# assume parameter vector W and its gradient vector dW param_scale = np.linalg.norm(W.ravel()) update = -learning_rate*dW # simple SGD update update_scale = np.linalg.norm(update.ravel()) W += update # the actual update print update_scale / param_scale # want ~1e-3 Activation / Gradient distributions per layer
错误初始化会减慢甚至停止学习过程。绘制所有层的激活/梯度直方图,观察输出分布。例如 tanh,希望分布在[-1,1],而不是全输出 0,或集中在两端。- First-layer Visualizations
处理图像时,绘制第一层特征。
- 左:特征为噪声,可能网络没收敛,学习率设置不当,权重正则化惩罚非常低。
- 右:清楚的特征,训练很好。
4. Parameter updates
反向传播计算梯度,梯度用于执行参数更新。
- 初版 SGD
沿梯度反方向,步长为学习率。(梯度是增加的方向,我们希望最小化 loss。)SGD:梯度直接改变位置。# Vanilla update x += - learning_rate * dx - SGD Momentum
收敛率高。loss 可以理解为丘陵高度,参数随机初始化相当于在某位置放一个初速度为 0 的点。优化的过程就是模拟点在山坡上滚动。这个点所受的力,就是损失函数的梯度,即梯度和加速度成正比。SGD 中梯度直接对位置进行积分。而动量中,梯度直接影响的是速度,间接影响位置。即除了步长和方向外,引入了摩擦力影响运动。# Momentum update v = mu * v - learning_rate * dx # integrate velocity x += v # integrate position其中 v 初始化为 0,mu 是动量,值为 0.9,物理意义和摩擦系数一致,该变量抑制速度并降低系统动能,使该点在山脚停下来。
交叉验证时,mu 一般为[0.5, 0.9, 0.95, 0.99],和学习率衰减类似,摩擦系数在学习后期会增加,在多个 epoch 内从 0.5 到 0.99.通过动量更新,参数向量将在具有一致性梯度的任何方向上建立速度。 - Nesterov Momentum
最近流行,对凸函数有更强理论收敛,实践更好。
计算受动量影响后,新位置的梯度,而不是当前位置。用新位置的梯度更新参数。x_ahead = x + mu * v # evaluate dx_ahead (the gradient at x_ahead instead of at x) v = mu * v - learning_rate * dx_ahead x += v也可以写成
v_prev = v # back this up v = mu * v - learning_rate * dx # velocity update stays the same x += -mu * v_prev + (1 + mu) * v # position update changes form - Annealing the learning rate
训练时,随时间推移减小学习率,因为高学习率的情况,参数动能大,无法稳定在损失函数小的地方。关键在于如何减小学习率:缓慢衰减,将浪费计算量,很长时间没有改进;减的太快,系统快速冷却,无法达到最小位置。- 按 epoch 衰减:典型的每 5 个epoch降一半,或每 20 个epoch降 0.1;取决于问题和模型。实践中,先用固定学习率训练,看验证集 loss,当损失不降时,将学习率减半。
- 指数衰减:\ \(α=α_0{e^{−kt}}\) a 和 k 是超参,t 是迭代次数。(也可以用 epoch)
- 1/t 衰减:
\(α=α0/(1+kt)\) 实践:用 step decay,选择较慢的衰减,训练时间长点。
Second order methods 二阶方法
牛顿法,不常用- Per-parameter adaptive learning rate methods
上述方法对所有参数的学习率平等调整,还有些方法可以针对每个参数自适应调整。- Adagrad:
# Assume the gradient dx and parameter vector x cache += dx**2 x += - learning_rate * dx / (np.sqrt(cache) + eps)根据梯度的大小来调整每个权重的学习率:cache 和梯度 size 相同,梯度大的权重,学习率会小,更新不那么频繁的权重学习率会提高。缺点:单调递减的学习率更新过于激进,会过早停止学习。
- RMSprop:对 Adagrad 进行调整,试图降低其激进的、单调递减的学习率。使用梯度平方的移动平均值。
cache = decay_rate * cache + (1 - decay_rate) * dx**2 x += - learning_rate * dx / (np.sqrt(cache) + eps)decay_rate 是超参数,取值 [0.9, 0.99, 0.999], RMSProp 仍然根据梯度的大小来调整每个权重的学习率,但不会单调。
- Adam:RMSprop + momentum
m = beta1*m + (1-beta1)*dx v = beta2*v + (1-beta2)*(dx**2) x += - learning_rate * m / (np.sqrt(v) + eps)使用原始梯度的平滑版本。eps = 1e-8, beta1 = 0.9, beta2 = 0.999。完整版本还包括 bias 校准机制,在最初时间步中,m 和 v 被初始化,bias 为 0,但 warm up 后不是。
# t is your iteration counter going from 1 to infinity m = beta1*m + (1-beta1)*dx mt = m / (1-beta1**t) v = beta2*v + (1-beta2)*(dx**2) vt = v / (1-beta2**t) x += - learning_rate * mt / (np.sqrt(vt) + eps)最终权重的更新还和迭代次数有关。虽然个体学习率会自适应,并不意味着全局学习率不用衰减。
- 左:不同优化算法的损失表面和时间演化的轮廓。请注意基于动量的方法的“超调”行为,这使得优化看起来就像一个球从山上滚下来。
- 右:优化过程中鞍点的可视化,其中沿不同维度的曲率具有不同的符号(一个维度向上弯曲,另一个维度向下弯曲)。请注意,SGD 很难打破对称性并卡在顶部。相反,RMSprop 等算法会在鞍座方向看到非常低的梯度。由于 RMSprop 更新中的分母项,这将增加沿该方向的有效学习率,帮助 RMSProp 继续进行。
- Adagrad:
5. Hyperparameter optimization
最常见的超参数:
- 初始学习率
- 学习率衰减 schedule(衰减常数值)
- 正则强度(L2 penalty, dropout 强度)
不太敏感的超参数:自适应学习率中的动量设置和时间表。
本节介绍超参数搜索:
- Implementation.
较大的网络通畅要训练好几天,因此超参数搜索可能需要几周,这会影响代码基础设计。一种方案是 worker + master。- worker:持续随机采样超参数,执行优化。在训练期间,worker 记录每个 epoch 验证集的表现,将 model checkpoint 写入文件,文件名为验证集性能。
- master:在计算集群中启动或终止 worker,并检查 checkpoint,绘制训练数据。
- 优先选择单折验证,而不是交叉验证
多数情况单个验证集相当大,可以简化代码,不需要多折的交叉验证。很多人说交叉验证了一个参数,实际上只用了单个验证集。 - Hyperparameter ranges.
在对数尺度上搜索超参数。学习率经典取样:learning_rate = 10 ** uniform(-6, 1)随机采样:从均匀分布中取随机数,然后以10为底数。对正则强度也采取同样策略取样。
dropout 的搜索不用10做底数。dropout = uniform(0,1)
展开来说:学习率和正则强度对训练的影响是通过乘法,如果学习率是10,那改变定值例如 0.01,基本没影响。所以学习率搜索通常做乘法和除法。 - Prefer random search to grid search.
随机搜索比网格搜索更高效,也更易实现。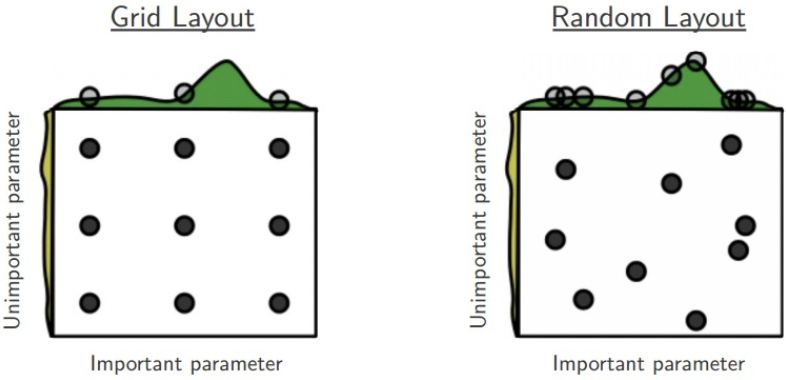
通常情况下,某些超参数就是比其他好,随机搜索可以更精确的发现重要超参数。
- Careful with best values on border.
有时超参数在一个不对的范围内搜索,例如从均匀分布中随机采样学习率时,最后记得检查下极值,因为区间两端点不在取值范围内。 - Stage your search from coarse to fine.
实践中,先在大概范围内搜索,然后根据最佳结果的取值,缩小搜索范围。
在第一个 epoch 内进行初始的粗粒度搜索,因为很多不正确的超参数设置会导致模型不学习,或loss爆炸。
第二阶段可以用 5 个 epoch 进行小范围搜索。
第三阶段用更多 epoch,在最终确定的小范围内进行详细搜索。 - Bayesian Hyperparameter Optimization
贝叶斯参数优化,核心思想是在探索不同超参数的表现时,平衡探索和剥削。库:Spearmint, SMAC, Hyperopt. 但是实践中,间隔搜索还是不如随机搜索。
6. Evaluation
- Model Ensembles
实践中,通过训练多个独立模型,在测试时算平均值的方式,来提高网络性能。随着集成模型数量的增多,性能通常单调提高。集成中模型的不同,使性能的提升更戏剧化。以下为塑造集成模型的方法:- Same model, different initializations.
交叉验证确定最优超参数,然后使用最佳的超参数训练多个模型,但随机初始化不同。缺点:变化仅由初始化引起。 - Top models discovered during cross-validation.
用交叉验证确定最佳超参,选效果最好的前10个模型作集成。改善了集成的多样性,且容易实现。 - Different checkpoints of a single model.
适用:训练花费高,多样性不足,但易实现。 - Running average of parameters during training.
一种低成本提升1-2个点性能的方式:把网络权重copy下来,其中包含训练时权重的指数衰减记录。取最后几个迭代,求权重的均值。这个平滑版本的集成权重在验证集的性能往往会更好,因为直觉上目标函数是碗状的,模型在曲线上来回跳,取最后几步的均值有更高的概率接近最低点。 - 集成的缺点:需要更长时间评估测试集。最新的思想是通过合并集成的 log likelihods 到一个修改后的目标,将集成蒸馏回单个模型。
- Same model, different initializations.
总结
为了训练一个神经网络:
- Gradient check:用一小批数据作模型的梯度检测,注意正则,dropout等。
- Sanity check:看初始 loss 是否合理,应当在一小部分数据上训练准确率 100%。
- During training:监控 loss,训练/验证 acc,甚至参数更新的幅度(~1e-3),第一层权重。
- 两个推荐优化器:Adam,SGD + Nesterov Momentum。
- 学习率衰减:例如在固定epoch后学习率减半,或一旦验证集准确率最高。
- 用随机搜索找最优超参数。现在更广的超参数范围搜索,训练 1-5 个epoch,然后缩小范围,训练更多轮。
- 通过模型集成提升性能。