CS231n: 6. Setting up the data and the model

太长不看

1. 必要预处理：减去平均值， 0 中心化。可选：除以标准差，归一化到 [-1, 1]。归一化：希望该分布方差为 1，让每个数据除以标准差。
2. 注意：0 中心化时，均值要仅在训练集上计算得出，然后验证和测试集再减去这个值。问题：处理缺失数据时呢？是对全局还是单训练集算？
3. PCA: 先 0 中心，算协方差矩阵（自己转置，乘自己，除以 size），然后对协方差矩阵做 SVD 分解，得到特征基向量 U。接着 X 和 U 的主成分点积，得到 X 基于大方差特征的变换，去相关。特征基 U 是变换的关键，通过 U 保留需要的特征，还可以将主成分特征旋转回原来的维度，做可视化。
4. [N x 3072] –> SVD 分解得特征基 U [3072 x 3072] –> 取前 144 个特征 U[:,144]，PCA 降维到 [N x 144] –> 后续做主成分可视化,乘上 U.transpose()[:144,:] 还原到图像原本尺寸。
5. 权重初始化：w = np.random.randn(n) * sqrt(2.0/n) 从均值 0 方差 1 的高斯分布随机采样，然后对方差归一化。用于有 ReLU 的网络，其中神经元方差为 2.0/n。
6. BatchNorm：在全连接层后，非线性层前。可以看做是在网络每一层进行预处理，提高对不良初始化的鲁棒性。强制让整个网络的激活为单位高斯分布。
7. L2 regularization：对权重平方惩罚。分散，小权重。
8. Dropout：加在所有计算后。训练时对网络随机采样，仅更新子网络部分的参数。测试时，计算所有子网络集成的平均。
9. 防过拟合：交叉验证 + L2 正则 + 每层 dropout(p=0.5)，p 根据验证集调。

1. Data Preprocessing

data matrix X: [N x D] (number of data, dimension)

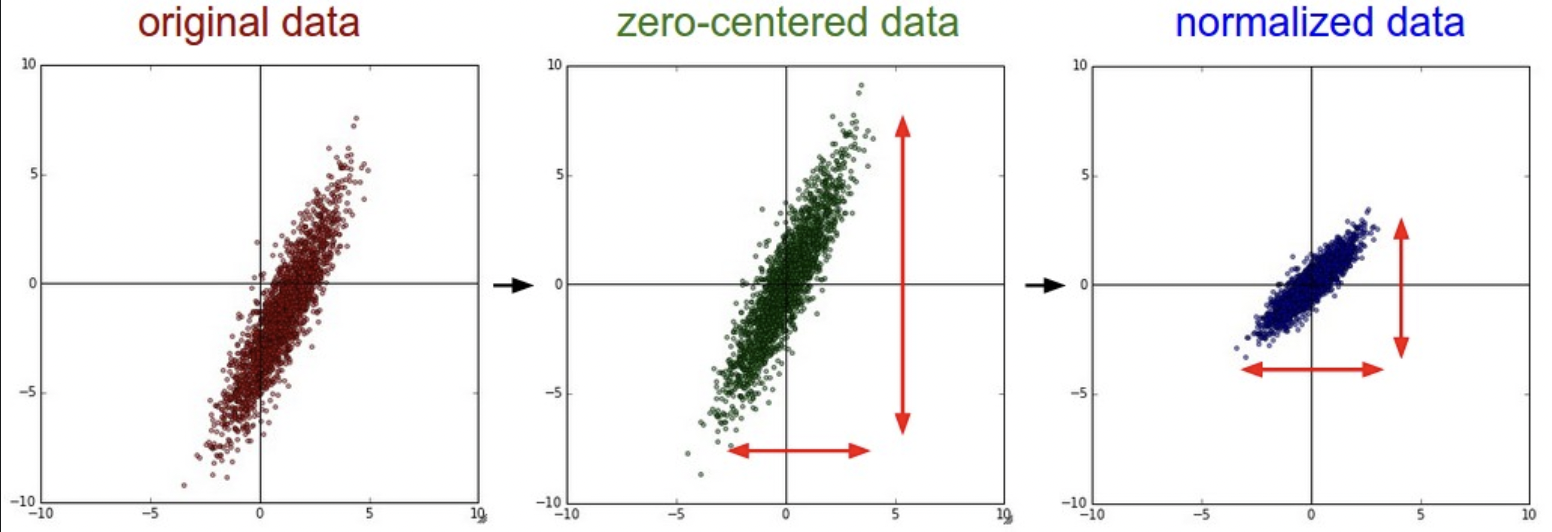
1. 减均值
   减去每个单独特征的均值。即 0 中心化。 zero-center。

   X -= np.mean(X)
   

2. Normalization
   让每个维度的尺度相同。两种方法。
   • 每个维度 0 中心后除以标准差。
   • 缩放到 [-1, 1] 归一化属于可选操作，适用于：不同输入特征的尺度不同，但对于结果有相同重要性。
     对于图像，尺度都是 [0, 255]，不归一化也行。

     X /= np.std(X, dim = 0)
     

     0 中心化本质是平移，用减法。归一化本质是缩放，用除法。

1. PCA
   先 0 中心，然后计算协方差矩阵。对角线是方差，对称，半正定。
   然后算协方差矩阵的 SVD 分解。U 的列 是特征向量。去相关：将原始数据投影到特征基中。即 X 和 U 做矩阵乘法。
   U 的列是正交向量，可以看做基向量。因此投射就是 X 的旋转，以特征向量为轴。SVD 分解中 U 的特征列是按特征值排序的，因此可以通过只使用前几个特征，对数据降维，并丢弃没有方差的维度。也就是 PCA 主成分分析降维。
   [N x D] –> [N x 100] 保留了含最大方差的 100 维数据。在 PCA 降维后的数据上训练，节省空间时间。

   # Assume input data matrix X of size [N x D]
   X -= np.mean(X, axis = 0) # zero-center the data (important)
   cov = np.dot(X.T, X) / X.shape[0] # get the data covariance matrix 
   
   U,S,V = np.linalg.svd(cov)
   
   Xrot = np.dot(X, U) # decorrelate the data
   
   Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced becomes [N x 100] PCA
   

2. whitening
   白化本质上归一化了尺度。将变换后的数据除以根号特征值。
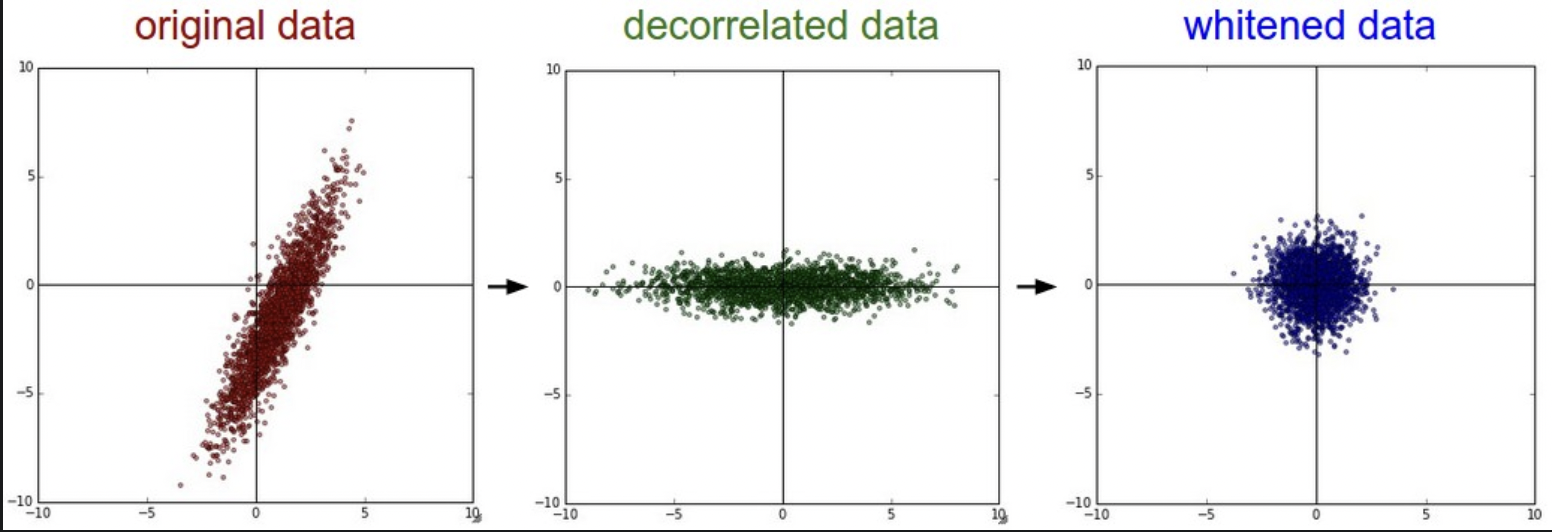
   如果输入数据是高斯分布，由白化归一化为均值 0，方差 1.会夸大噪声。

   # whiten the data:
   # divide by the eigenvalues (which are square roots of the singular values)
   Xwhite = Xrot / np.sqrt(S + 1e-5)
   

3. PCA 后，数据 0 中心，旋转到协方差矩阵的特征基。使数据去相关，即协方差为对角矩阵。 After performing PCA. The data is centered at zero and then rotated into the eigenbasis of the data covariance matrix. This decorrelates the data (the covariance matrix becomes diagonal)
4. 白化后，每个维度被缩放，协方差矩阵为单位矩阵。 Each dimension is additionally scaled by the eigenvalues, transforming the data covariance matrix into the identity matrix. Geometrically, this corresponds to stretching and squeezing the data into an isotropic gaussian blob.

1. 可视化
   CIFAR-10 部分数据 [49 x 3072]，每张图片拉伸到 3072 维行向量，协方差矩阵 [3072 x 3072]，取前 144 个特征向量，数据中的大方差对应低频。 PCA 降维后到 [49 X 144]，此时每个元素不再是亮度值，而是每个特征的叠加效果，不能直观可视化，要先旋转回 3072 个像素，乘上 U.transpose()[:144,:]。图像有点模糊，但保留大部分信息。
2. 实践：卷积网络不用 PCA，必要 0 中心，可选归一化。
3. 注意：预处理，例如均值，要在训练集上计算，然后应用于验证集和测试集。不能先在整体数据集计算均值，然后再划分。例如 0 中心化时，均值要在训练集上计算得出，然后每个划分减去这个值。

2. Weight Initialization

1. 注意：不能全初始化为 0。如果所有权重值相同，那所有梯度也相同，参数更新也相同了，就不存在非对称性了。
2. 小随机数：推测最终权重一半正，一半负，权重接近 0. randn 从均值 0，方差 1 的高斯分布中采样。W = 0.01* np.random.randn(D,H)
3. 权重不一定越小越好，因为小权重，梯度也会小，可能梯度消失。
4. Calibrating the variances with 1/sqrt(n)。
   随机初始化，方差会随数量增大而变大，所以要将方差归一化为 1，除以平方根。w = np.random.randn(n) / sqrt(n) 确保了神经元最初有基本相同的输出分布，加快收敛速度。
5. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification：在有 ReLU 的网络中用 w = np.random.randn(n) * sqrt(2.0/n) 做初始化。神经元方差为 2.0/n。
6. Sparse initialization. 初始化为 0，但是每个神经元和下方固定数量的神经元随机连接。例如 10 个。
7. In practice, the current recommendation is to use ReLU units and use the w = np.random.randn(n) * sqrt(2.0/n)
8. Batch Normalization
   在训练开始时，强制整个网络的激活为单位高斯分布。因为归一化是一种可微操作。
   实现：全连接层(或 Conv) –> BatchNorm 层 –> ReLU
   在全连接和非线性间 插入 BN 层。提高对不良初始化的鲁棒性。可以被解释为在网络每一层都做预处理，但以可微的形式集成到网络本身。

3. Regularization

控制网络容量，防过拟合。

1. L2 regularization
   最常见。在损失函数后加 参数的平方。整体除 2，求导梯度就直接是 λw 了。λ：正则化强度。W：网络中所有参数。
   \(\frac{1}{2} λw^2\)
   本质：惩罚大权重值，偏好分散的小权重。鼓励网络使用所有输入，而不是大量使用某些。梯度下降更新参数时：所有权重会线性衰减趋于 0，符合 W += -lambda * W。
2. L1 regularization
   λw。特性：权重变稀疏，趋于 0。具有 L1 正则化的神经元最终仅使用其最重要输入的 稀疏子集，并且对于“噪声”输入几乎保持不变。
   而 L2 正则是分散的，小权重。
3. Max norm constraints.
   对每个权重大小加上限，并用投射梯度下降加强约束。优点：学习率很大网络也不会爆炸，因为有上限。
4. Dropout
   训练时，有概率 p 让神经元启用，或为 0. 代码实现：乘上一个 mask: rand < p
   即训练时对网络随机采样，仅更新子网络部分的参数。测试时，计算所有子网络集成的平均。就是正常算，激活时乘 drop ratio p。
   在预测时不 drop，而是对隐藏层输出按概率 p 缩放。即测试时的输出，和训练时的预期输出相同。
   注意：实践时常用反向 dropout，因为测试性能很关键，把缩放 p 的操作放到训练执行，改为 除以 p，这样测试就不用额外操作了。

""" Vanilla Dropout: Not recommended implementation (see notes below) """

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  """ X contains the data """
  
  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = np.random.rand(*H1.shape) < p # first dropout mask
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = np.random.rand(*H2.shape) < p # second dropout mask
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3
  
  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)
  
def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations
  H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations
  out = np.dot(W3, H2) + b3

""" 
Inverted Dropout: Recommended implementation example.
We drop and scale at train time and don't do anything at test time.
"""

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = (np.random.rand(*H1.shape) < p) / p # first dropout mask. Notice /p!
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask. Notice /p!
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3
  
  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)
  
def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  out = np.dot(W3, H2) + b3

1. Theme of noise in forward pass
   包括 dropout, dropConnect：一组随机权重设置为 0. 随机池化，数据增强等。
2. Bias regularization.
   不常见，但也能提升性能。
3. Per-layer regularization.
   很少。
4. 实践：交叉验证 + L2 正则 + 每层 dropout(p=0.5)，p 根据验证集调。

4. Loss functions

1. 正则化 loss，看作对模型复杂度的惩罚。
2. data loss：监督学习中，衡量预测和真实值之间的兼容性。
3. 分类任务：
   • SVM: 正确类比其他类高出一个定值。
   • Softmax: cross-entropy loss。-log（e的次方） 需要分的类很多时，用层级结构 Hierarchical Softmax：例如英语字典，用 Tree path，训练每个节点的分类器。
4. Attribute classification
   不止一个类别，例如社交媒体上的图片，有很多 hashtag。此时为每个属性训练一个二分类器。正样本分数小于1，或负样本大于-1，就会累积梯度。
5. Regression
   预测实值，计算预测值和 gt 的差异，衡量差异用 L2 或 L1.
   用 L2 的原因是平方操作会简化梯度，L1 则对每个维度的绝对值求和。
   注意：
   • L2 loss 比 softmax 更难优化，因为需要网络有特定属性，为每个输入精确输出一个正确值。而 softmax 中每个分数的精确值不重要，重要的是相对大小。
   • L2 loss 鲁棒性较差，因为异常值会引入大梯度。
   • 处理回归问题时，先考虑能否转为分类问题，构建多个分类器。例如：预测产品星级。用 5 个独立的分类器得到 1-5 星的评级。分类提供了回归输出的分布，不局限于没有表明置信度的单个输出。
   • 如果不能转为分类，使用 L2 loss，但谨慎 dropout。

   When faced with a regression task, first consider if it is absolutely necessary. Instead, have a strong preference to discretizing your outputs to bins and perform classification over them whenever possible.

6. Structured prediction
   标签为任意结构，例如 graph，tree。
   结构 SVM loss：正确结构和得分最高的错误标签之间有固定差距。不是用梯度下降，而是设计特殊的求解器，利用结构空间的特定假设。

总结

1. 预处理：减去平均值，0 中心化。+ 除以标准差，归一化到 [-1, 1]
2. 用 ReLU + 带归一化的随机初始化 w = np.random.randn(n) * sqrt(2.0/n)
3. L2 regularization + dropout 防过拟合。
4. batch normalization：more robust to bad initialization
5. 分类 loss：SVM, softmax
6. 回归 loss：L2, L1