CS231n: 5. Architecture, ReLU, overfitting

太长不看

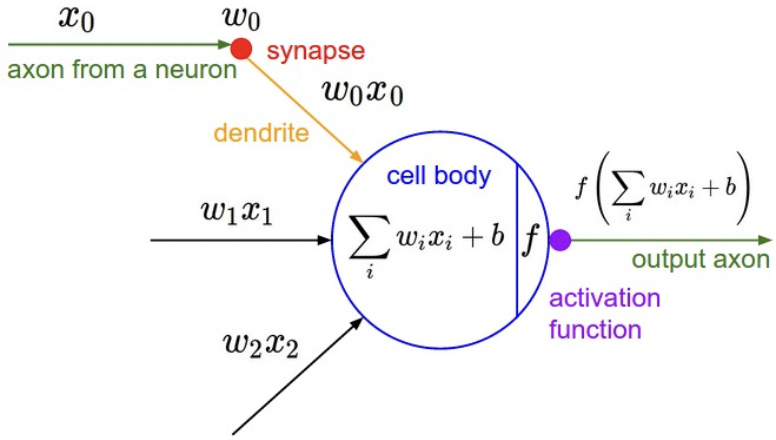
• synapse: 突触
• dendrites: 树突
• axon: 轴突（单个，会分叉
  1. 从树突接收信号，沿轴突产生信号，从突触发到别的树突。
     1 号：轴突 产生信号 x –> 突触强度 W –> 2号：树突 Wx –> 细胞体 sum。如果总和 大于阈值，fire，
     激活函数 f 模拟 spike 的频率 –> firing_rate = f(Wx + b)
  2. 问题：这个阈值是什么？高于阈值该神经元被激活。为什么激活函数是频率？激活发生在细胞体？隐藏层大小根据什么设置？
  3. 频率包含信息？例如位置编码，00，01，10，11 每个位变化的频率是不同的。不同频率的组合，表达信息。
  4. 神经网络：分层的无环图结构。输入不算层数。即单层网络只有输入输出。
     本质上是矩阵乘法和激活函数。
     指标：神经元数量，参数量计算。
     为什么用多层：实践经验。卷积网络中，更深识别效果更好。
  5. 激活函数选 ReLU。加速收敛。
  6. 大网络 + 强正则化 解决过拟合。
     大网络局部最优多，但每个局部最小值 loss 小，总体 loss 方差小，不依赖初始化。小网络泛化更强，但难训练，容易陷入很差的局部点。
     大网络拟合能力强，但容易过拟合训练集。过拟合：模型拟合能力过强，导致高度拟合了噪声数据。
  7. 一句话，不要为了防过拟合而用小网络。应当在算力范围内，用尽可能大的网络，用各种正则化技术控制过拟合。weight decay, dropout.

1. Quick intro

1. 线性分类部分中，用 s = Wx 计算图像的类分数，x 是图像所有像素的列向量。CIFAR10 x [3072, 1]，W [10, 3072]，输出是 10 个类的分数向量。
2. 神经网络中，s = W_2 max(0, W_1x), W1 是 [100, 3072]，将图像转换为 100 维中间向量。max(0,−) 是非线性函数，将所有小于 0 的激活 阈值设置为 0. 最后用 W2 [10, 100] 转回 10 类分数。
3. 非线性很关键，如果没的话，两个矩阵就等同单个矩阵了，那就还是线性映射。
4. The non-linearity is where we get the wiggle. 权重 W1 W2 通过 SGD 学，梯度用反向传播算。
5. 三层神经网络 s = W3 max(0,W2 max(0,W1x)), 隐藏层的向量大小是超参。

2. Modeling one neuron

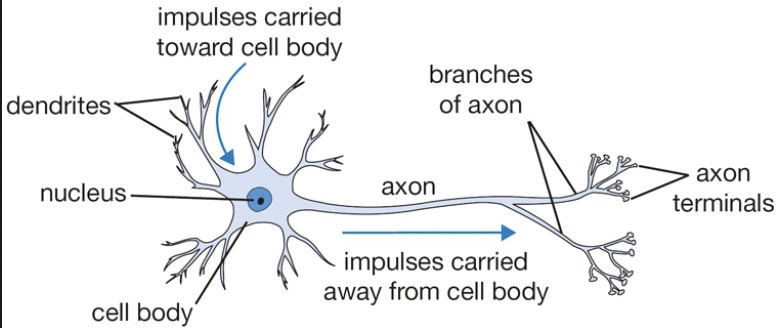
• synapse: 突触
• dendrites: 树突
• axon: 轴突（单个，会分叉 If the final sum is above a certain threshold, the neuron can fire, sending a spike along its axon.
  1. Biological motivation and connections: 大脑的基本计算单元是神经元。神经系统有 860亿 个神经元，和 10^14 个突触相连。每个神经元从树突接受输入信号，沿轴突产生输出信号。轴突最终分支，通过突触连接到其他神经元的树突。计算时，轴突传播的信号为 x，另一个神经元树突的强度为 W，通过乘法交互。该假设认为，突触强度 W 是可学习的，控制神经元对另一个神经元的影响强度，例如兴奋或抑制。
  2. 然后树突将信号传到细胞体，求和。如果总和高于某个阈值，神经元放电，沿着轴突发送一个峰值。假设尖峰频率传递信息，用激活函数模拟神经元的放电速率，表示沿轴突的尖峰频率。
  3. 激活函数通常用 sigmoid，输入是求和后的信号强度，压缩到 0-1范围。
  4. 一句话，每个神经元对输入 x 执行 f(Wx+b)
  5. 这种建模很粗糙，树突执行复杂的非线性计算，突触也不单是个权重，而是复杂的非线性系统。因此神经网络和真实大脑差距很大。

3. Single neuron as a linear classifier

单个神经元可以实现二元线性分类器：

1. 二元 Softmax 分类器：激活后的取值为 0-1，看作类概率。二分类，大于 0.5 就预测为该类。
2. 二元 SVM 分类器：神经元的输出加个 hinge loss。
3. 正则化解释：生物视角中，regularization loss 看作 gradual forgetting。让每次参数更新后，所有突触权重 W 趋于 0，就逐渐忘掉了。 A single neuron can be used to implement a binary classifier (e.g. binary Softmax or binary SVM classifiers)

4. Commonly used activation functions

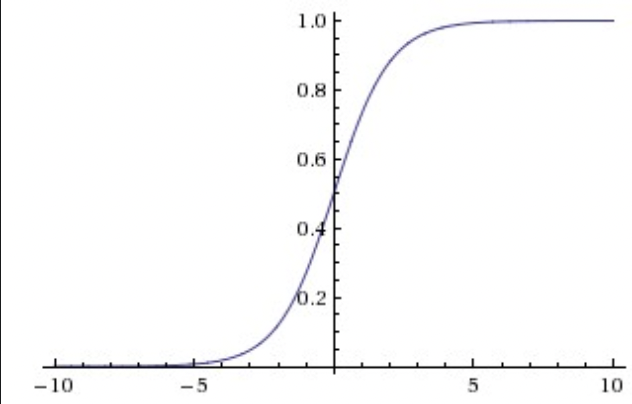
1. Sigmoid
   压缩到 0-1 范围，对神经元的 firing rate 有很好解释：从完全不 fire 到最大频率 fully-saturated firing。现在很少用了。
2. Sigmoids saturate and kill gradients.
   在靠近 0 和 1 区域的梯度为 0. 由于反向传播时，当前门对最终输出的梯度 要乘 局部梯度，这个局部梯度为 0，导致没梯度传下去，网络不学了。
   因此权重初始化时要注意，不要过大过小，导致饱和。
3. Sigmoid outputs are not zero-centered.
   输出会非 0 中心，影响权重 W 的梯度，反传时梯度全为正，或全为负。导致 undesirable zig-zagging dynamics in the gradient updates for the weights。batch 里问题不大。

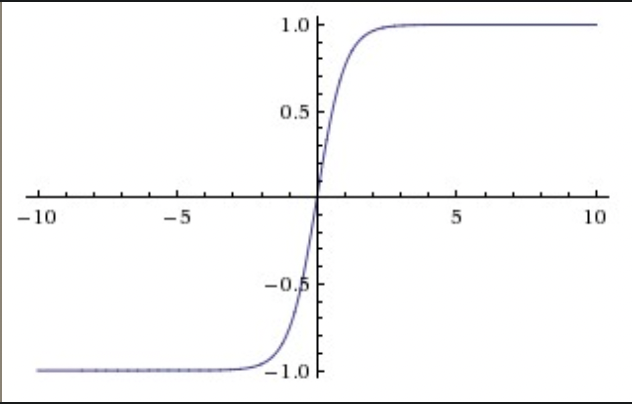
1. Tanh
   [-1, 1] 范围，0 均值。同样有饱和问题。实践中优于 Sigmoid，本质上是 Sigmoid 的缩放。
   \(tanh(x)=2σ(2x)−1\)

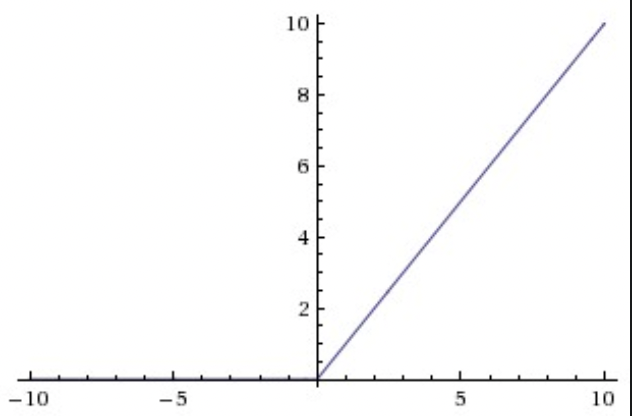
1. ReLU
   Rectified Linear Unit
   \(f(x) = max(0, x)\)
   本质：激活阈值为 0.
   • 加速 SGD 收敛，可能由于线性，非饱和。
   • 运算简单。
   • 训练中可能死掉。假如一个很大的梯度 流过 ReLU 神经元，权重会更新，但是这个神经元不会再激活，后续梯度为 0。也可能因为 学习率过大。我的理解是 给饿死了，因为负输入为 0。
2. Leaky ReLU
   解决饿死的问题。负输入时，乘上一个很小的系数。褒贬不一
   \(f(x) = αx (x < 0)\)
3. Maxout
   \(max(w^T_1 x + b_1, w^T_2 x + b_2)\)
   本质是 ReLU 的推广，参数量翻倍。
4. 激活函数选择：ReLU 就完了。

Use the ReLU non-linearity, be careful with your learning rates and possibly monitor the fraction of “dead” units in a network.

If this concerns you, give Leaky ReLU or Maxout a try. Never use sigmoid. Try tanh, but expect it to work worse than ReLU/Maxout.

5. Neural Network architectures

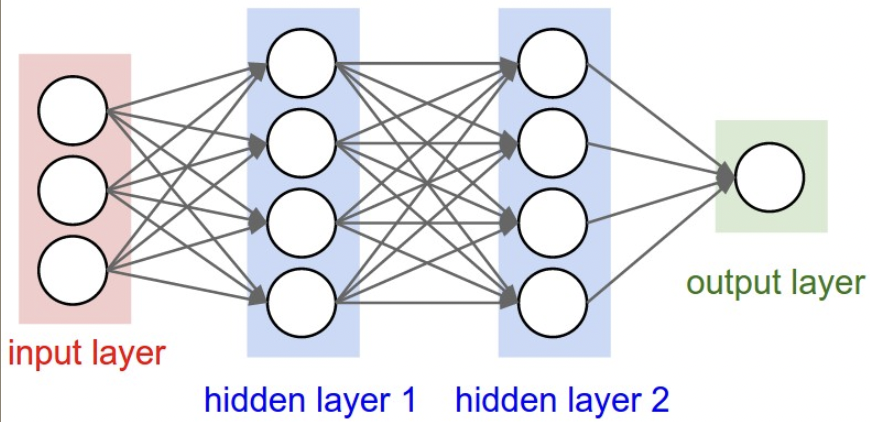three-layer neural network

1. Layer-wise organization
   本质: 无环图结构。通常分层。
   全连接层：两个邻层间的神经元全部成对连接，层内无共享。
2. 命名
   N 层神经网络，意味着不包括输入层。例如单层网络，实际上只有输入输出，没有隐藏层。等同于 SVM 或逻辑回归。也被叫做 MLP。
3. 输出层
   不用激活函数，因为是类分数。
4. 神经网络大小
   衡量指标：神经元数量，参数量。
   例图中：
   • neurons = 4 + 4 + 1
   • weights = [3 x 4] + [4 x 4] + [4 x 1]
   • biases = 4 + 4 + 1
   • learnable parameters = weights + biases 现在卷积网络通常 100 million 参数，10-20 层。the number of effective connections is significantly greater due to parameter sharing.

6. Example feed-forward computation

1. 本质上是矩阵乘法 和 激活函数。输入是 batch column vector The forward pass of a fully-connected layer corresponds to one matrix multiplication followed by a bias offset and an activation function.

7. Representational power

1. 有全连接层的神经网络：理解为定义了一个函数族。由权重参数化。
2. 神经网络可以逼近任何连续函数。
3. 既然单层就可以近似任何函数，为什么需要多层？实践经验。

Neural Networks work well in practice because they compactly express nice, smooth functions that fit well with the statistical properties of data we encounter in practice, and are also easy to learn using our optimization algorithms (e.g. gradient descent).

1. 实践中 3 层 通常比 2 层好，但更深影响不大。
2. 但在卷积网络中，更深识别效果更好，例如 10 层。因为图像包含层级结构，例如 face 由 eyes 组成，眼由边缘组成。several layers of processing make intuitive sense for this data domain.

8. Setting number of layers and their sizes

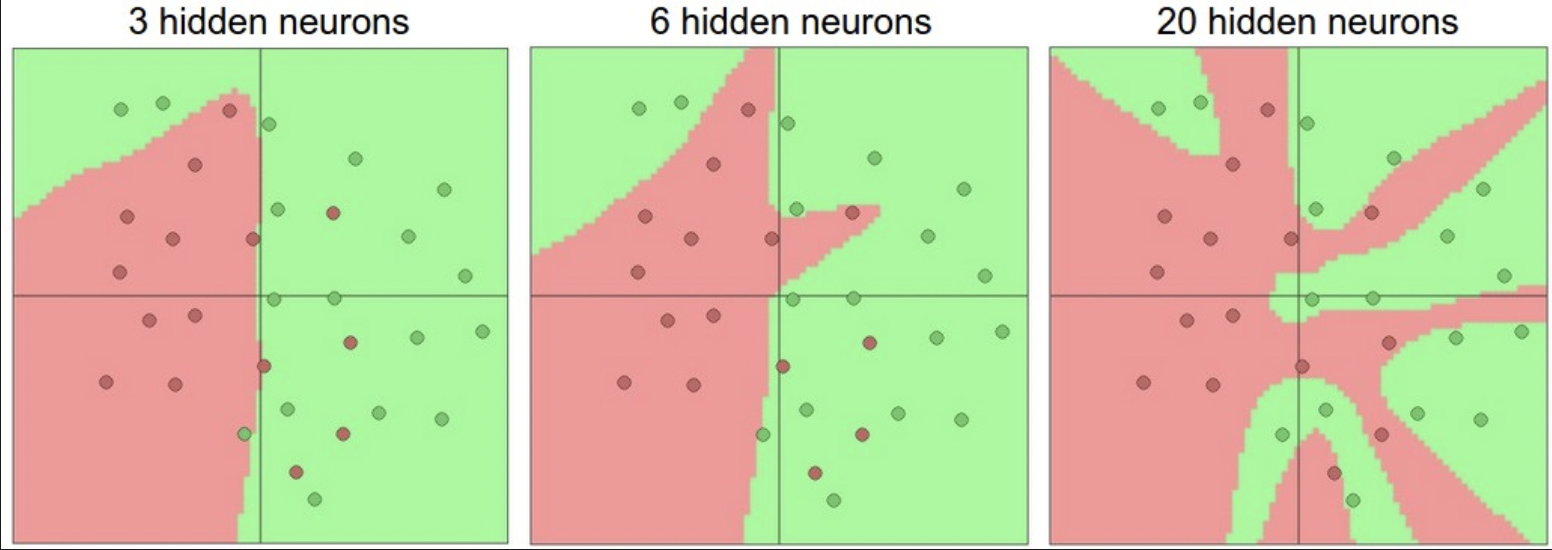
1. 用几层？每层多大？网络容量会改变，导致表达能力变强，可以拟合更复杂的函数。但同时，也更容易过拟合训练集。
2. 过拟合：模型拟合能力过强，导致高度拟合了噪声数据。
3. 例如图中 20 个神经元，拟合了所有训练数据，但代价是把向量空间分成了很多不联合的区域。3 个神经元的表达能力只够大概分一下，把类外的数据解释为噪声，这在测试集中有更好的泛化。better generalization on the test set.
4. 似乎对于不复杂的数据，用小网络不容易过拟合，但这不对。实践中应该优先采用防过拟合的方法，例如 L2 regularization, dropout, input noise，而不是控制网络大小。
   因为小网络更难用 SGD等局部优化训练，虽然小网络 loss 的局部最小值少，但是局部最小值容易收敛，且 loss 很高。而更大的网络有更多 local minima，这些局部最小值的 loss 会小。
   神经网络是非凸函数。实践中，小网络 loss 方差很大，可能收敛到 good place，也可能困在很差的局部值。而大网络方差小，即所有结果都差不多，且不过多依赖初始化。
5. 正则化强度是控制过拟合的首选方案。regularization strength 越高，越平滑。

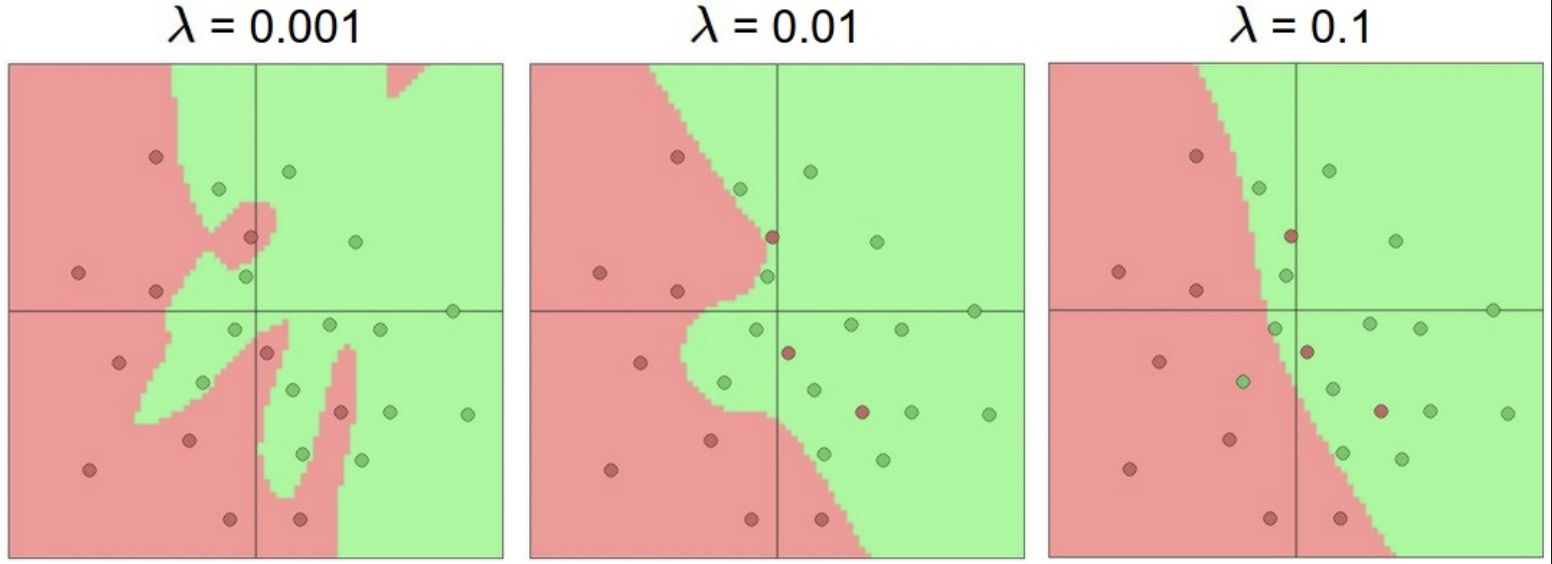
一句话，不要为了防过拟合而用小网络。应当在算力范围内，用尽可能大的网络，用各种正则化技术控制过拟合。

总结

1. 神经网络是通用函数逼近。They are used because they make certain “right” assumptions about the functional forms of functions that come up in practice.
2. 大网络总比小网络好，但较大容量意味着更强正则化约束，例如 weight decay，dropout，来防止过拟合。