CS231n: 4. Backpropagation

太长不看

1. 电路角度：正向传播会计算 门的输出对输入的局部梯度，
   反向传播拿到最终结果对门的梯度，从后向前通过链式法则，乘上 forward pass 算的局部梯度，得到输出对输入的完整梯度。
2. 导数：函数 在特定无限小区域 变量 的变化率。
   当变量非常小，近似于直线的斜率。某个变量的导数，意味着整个表达式 对这个值变化的 敏感性。
3. sigmoid 求导 = (1−σ(x))σ(x)
4. 乘法门有个问题：如果一个输入很小，另一个很大，乘法门就会给小输入分配一个大梯度，给大输入分配小梯度。线性分类器中 Wx 权重和输入相乘，导致输入数据 x 的数值大小 对权重 W 的梯度大小有影响。
   假设预处理时 所有输入数据 x 都乘 1000，那权重 W 上的梯度 会扩大 1000 倍，梯度大意味着很陡峭，导致必须减小学习率来补偿影响。意味着预处理很重要。
5. 多变量 梯度在分叉处累积。
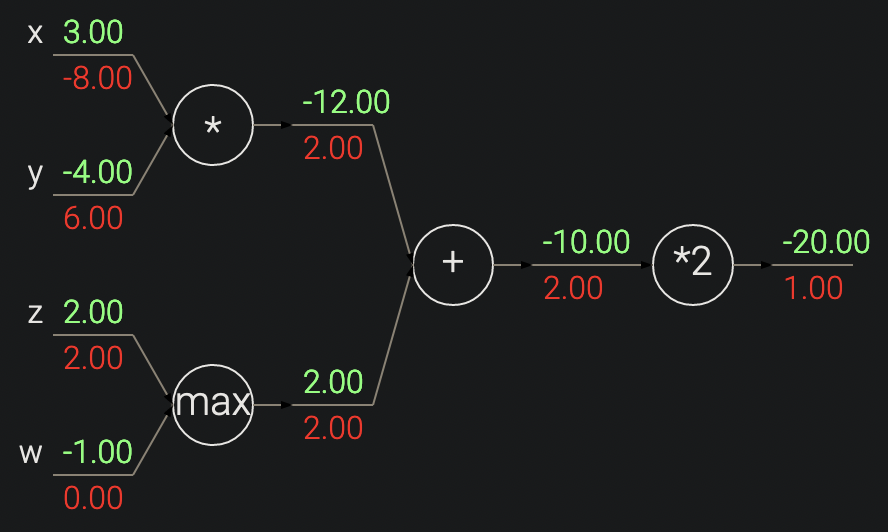
6. 反向梯度流动
   • Add 将梯度均分给所有输入
   • Max 将梯度流向最大的输入
   • Multiply 局部梯度是对方的输入值。

阶段总结

1. 明确图像分类问题：图像就是由像素描述的多维空间中的一个点，给这个点分配标签。输入：列向量 [3070 x 1]
2. 考虑两个问题，如何把这个点映射到标签，最简单：假设线性 y = Wx。如何评价映射的好坏：（交叉熵）Softmax loss = -log(p)。加正则化限制 W 大小，L2:所有权重的平方和。
3. 现在我们希望映射准确，要降低 loss，也就是优化损失函数，找到使 loss 最小的 权重 W。以 CIFAR10 为例，W 大小为 [10 x 3070]，每一行就是一个类的分类器。
4. 一个线性层 nn.Linear(in_features, out_features) 里面的矩阵 W 大小其实是 [out_features, in_features]，输入 x 大小为 [batch_size, in_features]。做的是矩阵乘法 xW_T。
5. 怎样优化呢？直接让导数=0不行，要沿着导数的反方向修改 W，因为梯度是 loss 下降最快的方向。一维求导叫斜率，多维向量每个维度求偏导，合起来就是梯度。梯度就是每个维度的偏导数。优化问题转换成了求 loss 对 W 的梯度。
6. 初始化 W0 先算一次 loss，然后更新一次参数要对应计算一次 loss。对整个训练数据算一次 loss 只更新一次 W 很慢，所以用 mini-batch。先随机初始化 W0，对一小批数据算 loss，迭代更新整体权重，这样一轮能更新很多次 W，每次更新的步长就是学习率。
7. 这里输入 x 到输出的整体 loss 函数很简单，是 Softmax 和 Wx 的复合函数。推广一下，换掉线性映射，如何对任意可微 loss 函数求梯度？求导链式法则：先正向传播，根据当前电路门输入输出计算局部梯度，然后反向传播，根据最终输出到当前门，和局部梯度，得到整个 输入到最终输出的梯度。
8. 更新下第2条，为什么对于语言和图像模型都说输出是从概率分布中采样呢？对于LM来说，语言建模要做的就是给一个序列分配概率。得到的 sequence of tokens 本来就是从模型的概率分布p中 sample 出来的，用条件概率来评价这个序列的好坏。而对于VM，以分类任务为例，最终输出的类别分数被 Softmax 归一化才得到了一个概率分布。使用交叉熵作为损失函数，即优化目标，衡量模型的预测分布和真实分布之间的差异。真实分布是gt的标签y，通常用 one-hot 向量形式表示，例如[0,1,0]，即y=1，因此交叉熵被简化为 -log(预测概率p)。
9. 最后一层分类器的线性矩阵W，可以把每一列看成单独一个类的分类器，也可以把每一列看成是一种模式，分类就是看哪个模板最匹配。
10. LM中word2vec的部分，本质上是将Index映射为向量。在 tokenizer 的词库中，做 token-ID。在 Embedding 中，做 ID- vector 的映射。（这部分和 one-hot 没关系吧？）

# calculate the loss
output = net(imgs)
loss = F.cross_entropy(output, classes)

optimizer.zero_grad()

# 反向传播
loss.backward()
# 更新参数
optimizer.step()

1. Introduction

1. Movitation.
   反向传播：递归应用链式法则，计算表达式梯度。
   问题：计算 f(x) 在 x 处的 梯度 ∇f(x)
   f 是损失函数，x 和 训练数据，权重 W 有关。
   通常只计算 关于参数 W 的梯度

2. Simple expressions and interpretation of the gradient

1. 导数：函数 在特定无限小区域 变量 的变化率。
   当变量非常小，近似于直线的斜率。另一个角度，某个变量的导数，意味着整个表达式 对这个值变化的 敏感性。
   he derivative on each variable tells you the sensitivity of the whole expression on its value. 梯度就是偏导向量。

3. Compound expressions with chain rule

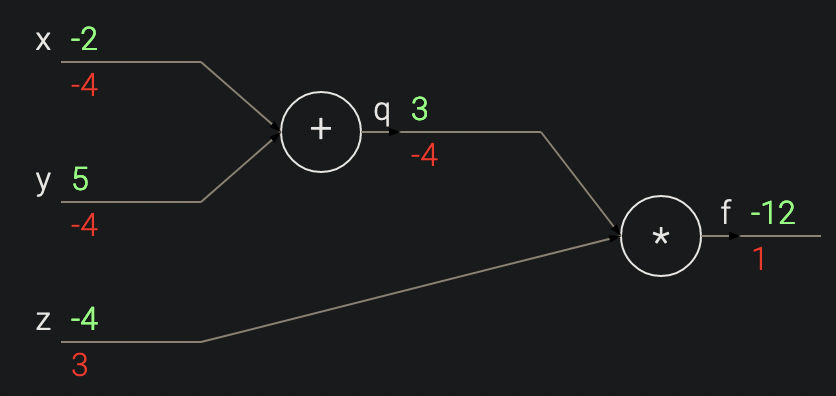
输入 [-2, 5], 输出 3，加法，两个输入局部梯度都是 1。最终输出是 -12。反向传播：加法门输出梯度是 -4，链式法则，输入梯度是 1 * -4 = -4. 如果 xy 输入减小，相应负梯度，加法门输出将减小，而乘法门输出增加。

1. 例：\(f(x,y,z) = (x+y)z\)
   复合函数，拆成 q = x + y, f = qz，求导链式法则：
   \(\frac{∂f}{∂x} = \frac{∂f}{∂q} \frac{∂q}{∂x}\)
   • forward pass: 计算输入到输出的值
   • backward pass: 反向传播从末尾开始，递归用链式法则计算梯度 直到输入。
     The gradients can be thought of as flowing backwards through the circuit.
     这里加法的导数是 1，乘法偏导数是另一个变量。

4. 反向传播直观理解

1. 反向传播是 局部 过程。
   向前传播：电路角度，每个门拿到输入，不用管其他部件，可以直接算 输出和局部梯度。
   反向传播：门拿到 自己的输出 在最终输出 上的梯度，然后乘上前向传播的局部梯度，得到输入到输出的整体梯度。
   This extra multiplication (for each input) due to the chain rule can turn a single and relatively useless gate into a cog in a complex circuit such as an entire neural network.
2. 反向传播：理解为电路门，期望输出增加或减少，使最终输出更高。

5. Modularity: Sigmoid example

1. 任意可微函数 都可以当作 gate。可以将多个门看成一个，也可以一分为多。
2. sigmoid 梯度计算很简单:
   \(σ(x)= \frac{1}{1 + e^{-x}}\)
   求导
   \(\frac{dσ(x)}{dx}=(1−σ(x))σ(x)\)
   例：x = 1，output = 0.73, dx = (1 - 0.73) * 0.73 = 0.2

6. 分阶段计算

1. 将函数分解成 几个便于计算局部梯度的部分。然后用链式法则。
2. 缓存向前传播过程中的有用变量。
3. 梯度在分叉处相加。注意多变量要用 += 累积每个分支上的梯度。即如果一个变量分支到电路的不同部分，那么流回它的梯度将会相加。

7. Patterns in backward flow

1. 直观解释向后流动的梯度：
   • Add 将梯度均分给所有输入
   • Max 将梯度流向最大的输入
   • Multiply 局部梯度是对方的输入值。
2. 不太直观的影响及其后果.
   乘法门有个问题：如果一个输入很小，另一个很大，乘法门就会给小输入分配一个大梯度，给大输入分配小梯度。线性分类器中 Wx 权重和输入相乘，导致输入数据 x 的数值大小 对权重 W 的梯度大小有影响。
   假设预处理时 所有输入数据 x 都乘 1000，那权重 W 上的梯度 会扩大 1000 倍，导致必须减小学习率来补偿影响。意味着预处理很重要。

8. 矢量化运算的梯度

1. 注意 dimensions and transpose operations.
2. Matrix-Matrix multiply gradient.

# forward pass
W = np.random.randn(5, 10)
X = np.random.randn(10, 3)
D = W.dot(X)

# now suppose we had the gradient on D from above in the circuit
dD = np.random.randn(*D.shape) # same shape as D
dW = dD.dot(X.T) #.T gives the transpose of the matrix
dX = W.T.dot(dD)