CS231n: 2. 线性分类器, SVM loss, Softmax

太长不看

1. score function 将原始数据映射标签。目前是线性映射，两种线性分类器用的 loss 不同。
2. 图像解释为高维空间中的一个点，线性分类器就是高维空间中的一条线。权重 W 每一行就是一个类的分类器
3. SVM 规定正确类的分数要高于其他类某个定值，用 ReLU loss。算 loss 要考虑其他类。
4. Softmax 分类器使用交叉熵作为损失，用 softmax 函数归一化，直观解释每个类的置信度。特性：e 的多少次方，总和为 1。分得更开更准，loss更小。
5. bias trick，将 bias 放到 权重矩阵 W 里一起训，输入 x 多加一列。
6. L2 正则化：loss 后加上 正则强度 λ * 权重的平方和，惩罚了大权重值，让权重值减小，weight decay。提高泛化能力，减少过拟合。
7. 图像数据预处理：必要 0 均值中心化。[0, 255] 每个特征减均值 ->[-127, 127]，后面可选 ->[-1, 1]
8. softmax loss 计算：-log(正确类的概率)，算 loss 只用考虑当前要预测的类。

1. Linear Classification

1. 回顾 KNN 缺点：要存储训练数据，测试逐个比较效率低。
2. 图像分类方法包括 2 个主要部分：
   • score function: raw data <–> class scores
   • loss function: predict scores <–> ground truth labels
3. 视为最优化问题，相对于 score function 的参数，最小化 loss。

2. Parameterized mapping from images to label scores

1. score function 定义：将像素映射到每个类别，置信度分数。
   例：CIFAR-10: 32 * 32 * 3 = 3072 个像素 映射到 10 个类
2. 线性分类器
   线性映射: \(f = Wx_i + b\) x: 像素个数 [3072 * 1], W: [10 * 3072], b: [10 * 1]
   通过W和b将 像素 线性映射为 标签。
   相当于权重矩阵W中每一行对应一个类的计算，每一行就是一个类的分类器。每个位置的权重，乘图像中对应位置像素点的值。

4 个像素，无关 RGB

3. Interpreting a linear classifier

1. 线性分类器要计算三个 Channel 的像素加权和，权重会影响颜色偏好，例如蓝色多，更可能是船。船分类器在 blue channel 正权重，RG 负权重，减小 score。
2. 将图像解释为高维空间中的一个点。
   例如，CIFAR-10 中的每个图像都是 32x32x3 像素的 3072 维空间中的一个点，整个数据集是一组点的集合。线性分类器就是高维空间中的一条线，线的一侧类别分数为正，线上 score = 0。

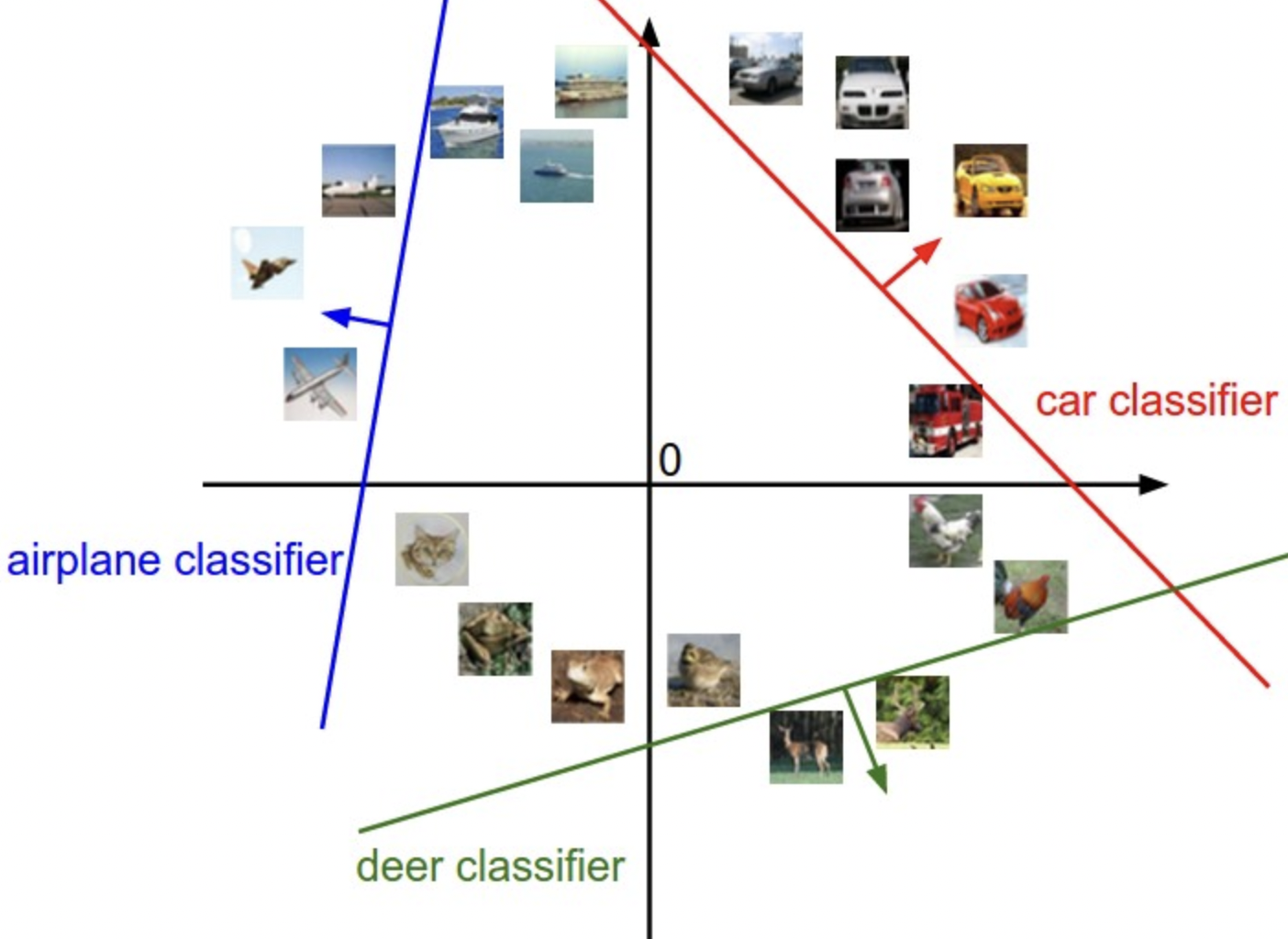
1. W每一行就是一个类别的分类器，整个权重矩阵类似上图可视化。改变W某一行，像素空间中的分类线会旋转。偏差b让分类线不经过原点。
2. 将线性分类器解释为模板匹配，模式是要学习的。
   W每一行对应一个类的模板。通过点积将图像和每个模板比较，找最适合的模板，得到每个类的分数。
   某种程度上也是最近邻，每个类用一个图像，用内积作为距离。

学到的权重可视化。船有大量蓝色像素。马头有左右，数据集中红色汽车最多。

1. 线性分类器很弱，无法解释不同颜色。而神经网络隐藏层中的神经元可以检测特定类型，下一层可以将上层输出做加权和得出分数。
2. Bias trick.
   输入多加一个常数列，将b移到W里一起学。最终只需要学一个权重矩阵。

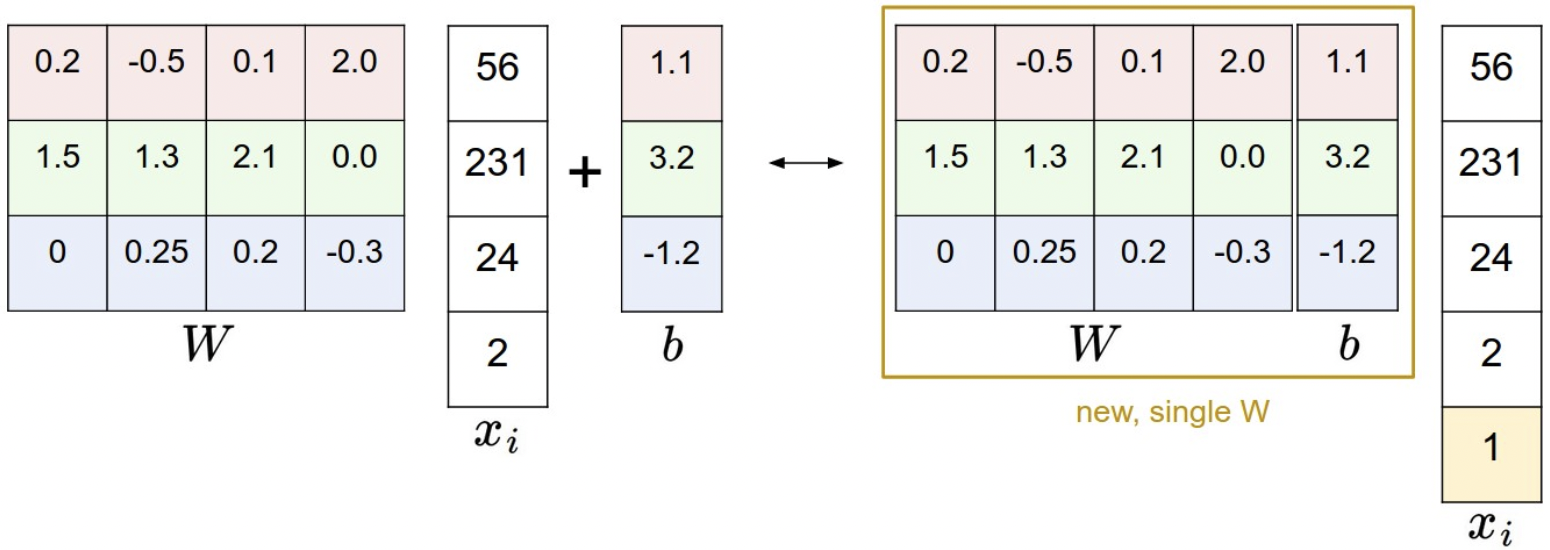
1. 图像数据预处理 对输入特征归一化，图像每个像素是一个特征: [0, 255]。每个特征减均值，让数据居中: [-127, 127]。然后缩放到 [-1, 1]。zero mean centering 零均值中心化很关键，影响梯度下降。

4. Loss function

1. score function 是将原始数据映射到标签分数的函数，通过改变权重值，使预测的类别分数和真实标签一致。用 loss function 衡量分类器好坏，分得好损失低。
   The loss function quantifies our unhappiness with predictions on the training set

5. Multiclass Support Vector Machine loss

1. 多类支持向量机损失函数。(SVM loss)
   SVM loss 希望正确类别的得分，比错误类别的，高出一个定值 Δ。 \(L_i=∑_{j≠y_i}max(0,s_j−s_{yi}+Δ)\) 正确类别的分数 至少要比 错误类别的分数 高出超参 Δ。否则，就是没区分度，积累该损失，也即这个差异还要高出多少才能满足超参。
   分得很开，loss = 0
2. hinge loss
   \(max(0, -)\) 0 阈值 threshold at zero。有平方版本，惩罚更高。
3. 可视化。
   约束：SVM 希望正确类别的分数比其他类至少高出 delta。如果在红色区域，就 accumulate loss，否则 loss 为 0. 目标是找到同时对所有训练样本满足此约束的权重 W，并且总 loss 尽可能低。

1. Regularization
   问题：满足约束的 W 不唯一，W 缩放一个大于 1 的值也满足约束。
   编码某些权重集 W 的偏好，来消除歧义。
   用正则化惩罚 扩展损失函数。最常见的 平方 L2 范数，对 W 的所有权重值进行平方惩罚，防止权重过大。 \(R(W)=∑_k∑_lW^2_{k,l}\)

   对 W 所有值的平方求和。正则化约束只和 W 的权重值有关，和数据无关。
   总 loss = data loss + λ * 正则 loss

   \[L=1/N∑_i∑_{j≠y_i}[max(0,f(x_i;W)_j−f(x_i;W)_{y_i}+Δ)]+λ∑_k∑_lW^2_{k,l}\]
2. 加正则化惩罚了大的权重值，提高泛化能力，减少过拟合。因为单独的输入维度不能对分数产生很大影响。
   例如 [1, 0, 0, 0] 和 [0.25, 0.25, 0.25, 0.25]，后者 L2 惩罚更小。
   L2 惩罚倾向于更小，更分散的权重矩阵。因此鼓励分类器弱考虑所有输入维度，而不是强少数。
3. bias 不会缩放输入值，也就不会控制输入的影响强度。所以通常只对 W 正则化。有正则化 loss 不可能为 0，除非 W 全 0.

def L_i_vectorized(x, y, W):
  """
  A faster half-vectorized implementation. half-vectorized
  refers to the fact that for a single example the implementation contains
  no for loops, but there is still one loop over the examples (outside this function)
  """
  delta = 1.0
  scores = W.dot(x)
  # compute the margins for all classes in one vector operation
  margins = np.maximum(0, scores - scores[y] + delta)
  # on y-th position scores[y] - scores[y] canceled and gave delta. We want
  # to ignore the y-th position and only consider margin on max wrong class
  margins[y] = 0
  loss_i = np.sum(margins)
  return loss_i

All we have to do now is to come up with a way to find the weights that minimize the loss.

6. Practical Considerations

1. 超参设置，delta = 1.0 就行。主要靠 正则化强度 λ。
2. Binary SVM：二分类特殊情况。

7. Softmax classifier

1. Softmax 是二元逻辑回归分类器在多个类上的推广。不同于 SVM 给出每个类的分数，Softmax 归一化类别概率，更直观。映射函数还是线性，但是分数解释为每个类的未归一化对数概率，用交叉熵损失替换 hinge loss。 \(L_i=−log(\frac{e^f_{y_i}}{∑_je^{f_j}})\) or equivalently \(L_i=−f_{y_i}+log∑_je^{f_j}\)

2. Softmax function. \(f_j(z)=\frac{e^{z_j}}{ ∑_ke^{z_k}}\) 将分数压缩到 0到1 之间，且总和为 1.
3. 信息论角度;
   真实分布 p 和 估计分布 q 的信息熵： \(H(p,q)=−∑_xp(x)logq(x)\) Softmax 分类器 最小化 估计的类别概率 和 真实分布 之间的交叉熵。
4. 概率解释:
   \(P(y_i∣x_i;W)=\frac{e^f_{y_i}}{∑_je^{f_j}}\) 解释为在权重 W 下分配到正确标签的概率。最小化正确类别的负对数似然，解释为执行最大似然估计。正则化解释为来自权重矩阵 W 上的高斯先验，执行最大后验估计。
5. 实际问题：数值稳定性
   除以很大的数会不稳定，要归一化。上下同减最大值。

f = np.array([123, 456, 789]) # example with 3 classes and each having large scores
p = np.exp(f) / np.sum(np.exp(f)) # Bad: Numeric problem, potential blowup

# instead: first shift the values of f so that the highest number is 0:
f -= np.max(f) # f becomes [-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f)) # safe to do, gives the correct answer

1. 可能令人困惑的命名约定
   SVM 用 hinge loss，Softmax 分类器用 cross-entropy loss。名称来自 Softmax 函数，将原始分数压缩为总和为 1 的归一化正值，以便使用交叉熵损失。

8. SVM vs. Softmax

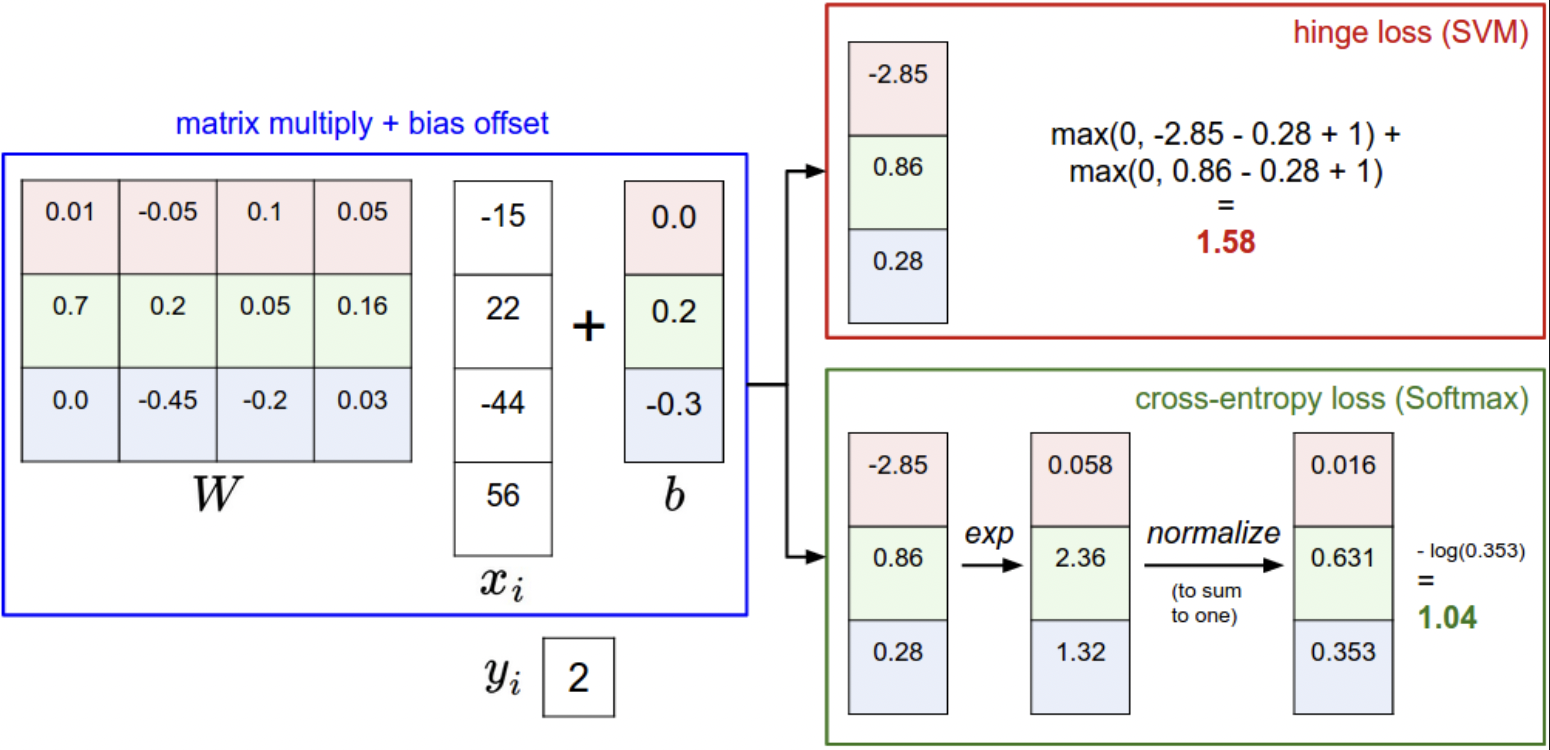
1. 差异在于 对分数的解释。
   SVM 解释为 类别分数，损失函数 鼓励 正确的类 分数比其他高。
   Softmax 分类器解释为对数概率，鼓励正确类的对数概率较高。
2. Softmax classifier provides “probabilities” for each class.
   SVM 分数不好解释，Softmax分类器直接计算标签概率，置信度。概率的分散程度取决于正则化强度 λ。正则化强，权重 W 变小，概率值会更分散。
3. 实践中，SVM 和 Softmax 通常具有可比性。
   性能差异小，与 Softmax 分类器相比，SVM 是一个更局部的目标。
   Softmax 分类器永远不会对其产生的分数完全满意：正确的类别总是具有较高的概率，而错误的类别总是具有较低的概率，并且损失总是会变得更好。然而，一旦满足边际，SVM 就会很高兴，并且不会对超出此约束的精确分数进行微观管理。这可以直观地被认为是一个特征：例如，一个汽车分类器可能将大部分“精力”花在将汽车与卡车分开的难题上，不应该受到青蛙示例的影响，它已经将青蛙分配得非常低得分，并且可能聚集在数据云的完全不同的一侧。

总结

1. score function 都是线性映射，两种线性分类器用的 loss 不同。
2. SVM 规定正确类的分数要高于其他类某个定值，用 ReLU loss。
3. Softmax 分类器使用交叉熵作为损失，用 softmax 函数归一化，直观解释每个类的置信度。特性：e 的多少次方，总和为 1。分得更开更准，loss更小。
4. bias trick，将 bias 放到 权重矩阵 W 里一起训，输入 x 多加一列。
5. 正则化惩罚了大权重值。提高泛化能力，减少过拟合。
6. 损失函数衡量预测质量，如何求得到最小损失的参数？如何优化？