卷积计算

推荐阅读: https://cs231n.github.io/convolutional-networks/

https://graphics.stanford.edu/courses/cs178/applets/convolution.html

https://blog.csdn.net/weixin_44064434/article/details/123647168

1. Feature_map

( 输入宽高 - 卷积核 + 填充 * 2 ) / 步长 + 1

例：input: [227, 227, 3], Conv2d(in_channels=3, out_channels=96, kernel_size=11, stride=4)

out = (227 - 11 + 0 * 2) / 4 + 1 = 55

output: [55, 55, 96]

1. 神经元个数：

` 55 * 55 * 96 = 290400 `

1. 参数量：

param = (11 * 11 * 3 + 1) * 96 = 34944

1. 多通道：
   每个 channel 有不同的卷积核，最终相加，channel=1. 例：输入 [227 x 227 x 3] -> 卷积核 [11 x 11 x 3 x 96]

卷积

卷积操作其实就是每次取一个特定大小的矩阵 F，然后将其对输入 X 依次扫描并进行内积的运算过程。

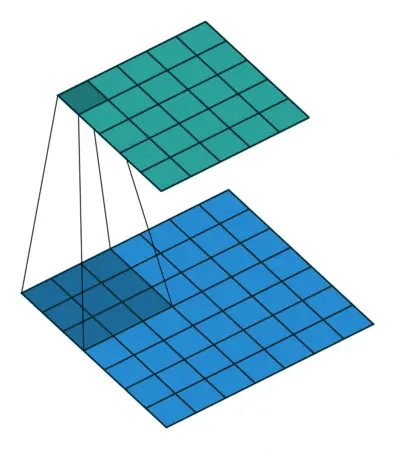
同时，我们将这个特定大小的矩阵 F 称为卷积核，即convolutional kernel或kernel或filter或detector，它可以是一个也可以是多个；将卷积后的结果 Y 称为特征图，即feature map，并且每一个卷积核卷积后都会得到一个对应的特征图；最后，对于输入 X 的形状，都会用三个维度来进行表示，即宽（width），高（high）和通道（channel）。

CNN 的 Inductive Bias 是 局部性 (Locality) 和 空间不变性 (Spatial Invariance) / 平移等效性 (Translation Equivariance)，即空间位置上的元素 (Grid Elements) 的联系/相关性近大远小，以及空间平移的不变性 (Kernel 权重共享)

前馈神经网络FNN，也叫深度前馈网络、多层感知机。目标是近似某个函数f 。 例如，对于分类器，y = f *（x）将输入x映射到类别y。 前馈网络定义映射y = f（x;θ），其中参数θ的值通过训练不断进行调整，使得函数更加拟合已知的结果。前馈神经网络叫前馈的原因：数据通过输入的x在定义的网络（f）中从前往后流动。这里面没有反向的传播，输出y无需再回到模型的输入位置再进行流动。

卷积神经网络有输入层、卷积层、激活函数、池化层、全连接层组成。卷积层用来进行特征提取；池化层对输入的特征图进行压缩，一方面使特征图变小，简化网络计算复杂度，另一方面进行特征压缩，提取主要特征；全连接层连接所有的特征，将信息输送给分类器（如softmax分类器）。

There is no learning done in max pooling layers, no weights or parameters to update just down sampling. However in convolutional layers there are weights that are learned so it down samples the data (if no padding is used) but it also extractes learned features. Usually both are used. A conv layer to extract features and a max pool to downsample and reduce the size of data.

多卷积核

对于一个卷积核，可以认为其具有识别某一类元素（特征）的能力；而对于一些复杂的数据来说，仅仅只是通过一类特征来进行辨识往往是不够的。因此，通常来说我们都会通过多个不同的卷积核来对输入进行特征提取得到多个特征图，然再输入到后续的网络中。