Vaniila Transformer

8 minute read

Published: October 07, 2024

手撕 Transformer

1. Tokenizer

2. Model details

Transformer 最初被提出用于解决 Seq2seq 翻译任务。如果要实现英文到德文的翻译，那么我们称英文为源语言，德文为目标语言。Transformer 的结构如下图所示，源文本的 embedding 与 positional encoding 相加后输入到 Encoder，经过 N 层 Encoder layer 后，输出在 Decoder 的 cross attention 中进行交互。目标文本的 embedding 同样与 positional encoding 相加后输入到 Decoder，Decoder 的输出通常会再经过一个线性层（具体取决于任务要求）。训练过程本质上是让模型学会什么时候结束这段话，学会何时输出<EOS>，相当于测试时贪婪的最后一步。src_input是<SOS>en_tokens<EOS>，tgt_input是<SOS>de_tokens，gt是de_tokens<EOS>.

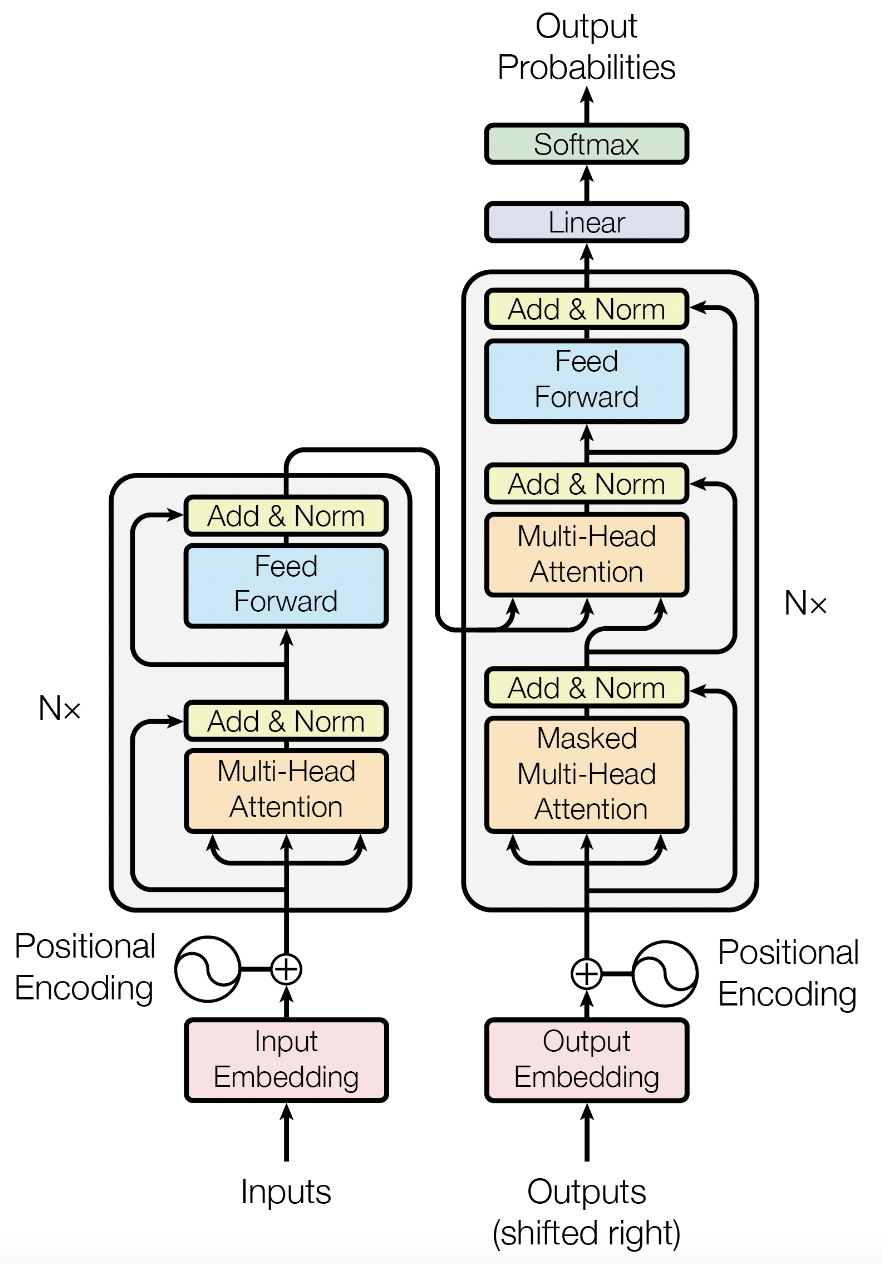
Encoder 和 Decoder 分别使用了两种 mask，src_mask 和 tgt_mask。src_mask 用于遮盖所有的 PAD token，避免它们在 attention 计算中产生影响，用于src和corss-attention（其中tgt是Q，src是KV）。tgt_mask 除了遮盖所有 PAD token，还要防止模型在进行 next word prediction 时访问未来的词。只用在tgt的自注意力。

Token Embedding

嵌入层里，有一个 embedding 矩阵 (\(U\in R^{C\times d_{model}}\)), \(C\) 为词典大小vocab_size，将输入的src_token_id转换成对应的 Vector，即嵌入空间的向量表示，其中语义相近的向量距离会更近。具体来说，Embedding one-hot 向量对 \(U\) 的操作是“指定抽取”，即取出某个 Token 的向量行。

self.tok_emb = nn.Embedding(vocab_size=vocab_size, d_model=d_model, padding_idx=pad_idx)

Positional Encoding

位置编码详解
由于 Transformer 不像 RNN 那样具有天然的序列特性，在计算 attention 时会丢失顺序信息，因此需要引入位置编码。原文使用固定的位置编码，用正余弦组合代表一个顺序。计算公式如下：

对于偶数维度:
\[\text{PE}(pos, 2i) = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)\]
对于奇数维度:
\[\text{PE}(pos, 2i+1) = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)\]

为了数值稳定性，我们对 div term 取指数和对数，即：

\[\text{div-term} = 10000^{2i/d_{\text{model}}} = \exp\left(\frac{2i \cdot -\log(10000)}{d_{\text{model}}}\right)\]

类比二进制表示一个数字，本质是不同位置上数字的交替变换，其中变换频率不同。

同时使用正弦和余弦：

让模型获取相对位置，因为对任何固定偏移量 \(k\), \(pos+k\) 的位置编码可以被表示为 \(pos\) 位置编码的线性方程。

\(pos\)：单词在一句话中的位置，取值范围：[0:max_len]
\(i\)：单词的维度序号，取值：[0:d_model]

位置编码和输入序列无关，只要模型的超参数确定，pos_enc就确定了，是一个大小为 [max_len * d_model]的矩阵，序列输入时，取前 [seq_len , d_model] 的部分。然后根据广播机制与 shape 为 [batch_size, seq_len, d_model] 的 token_emb 相加，得到 Encoder 的输入，记作 \(x_0\).

固定的位置编码对任何序列都是相同的，虽然依靠 max_len 和 d_model 生成，但是具有可扩展性。相同位置的编码不会受 max_len 影响,如果输入序列长度超出 max_len ，只需加上对应长度的位置编码。d_model 8 —> 4，相当于保留前半部分。

We chose the sinusoidal version because it may allow the model to extrapolate to sequence lengths longer than the ones encountered during training.

再补充一下，关于position encoding的思考。好处主要两点。第一，sin, cos函数保证值域[-1,1]，不会抢了词向量的风头。第二，这种编码方式，哪怕不同长度的文本，同样差两个字，差值也是相同的。但是，也带来了问题。sin(pox/x)，x决定了波长，波长过大，则相邻词的差值不明显，过小的话，则长文本必然会经过几个波，导致不同位置的有着相同值。transformer虽然最后用了不同维度不同波长，sin cos轮着来，来解决这个问题。但个人感觉并没有特别strong的数学理论依据，所以全用sin，全用cos说不定也是可以的。以及后期bert用的position embeding也说明这种方法不一定真的特别好用。

代码实现：

位置矩阵和输入无关，只和该点的坐标有关，枚举 pos_enc 的行列坐标，计算赋值。

max_len 指数据集里最长的一句话的 token 数，每个 batch 之间的 seq_len 可以不同，只要保证 batch 内 padding 到一样长就行。

class PositionalEncoding(nn.Module):
    def __init__(self, d_model, max_len=256):
        super(PositionalEncoding, self).__init__()

        # Initialize position encoding matrix (shape: [max_len, d_model])
        pe = torch.zeros(max_len, d_model)

        # Create a tensor of shape [max_len, 1] with position indices
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(
            1
        )

        # Compute the div_term (shape: [d_model//2]) for the sin and cos functions
        div_term = torch.exp(
            torch.arange(0, d_model, 2).float()
            * (-math.log(10000.0) / d_model)
        )

        # Apply sin/cos to even/odd indices in the position encoding matrix
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)

        # Register pe as a buffer, not a parameter (no gradients needed)
        self.register_buffer("pe", pe)

    def forward(self, x):
        batch_size, seq_len = x.size()
        # [seq_len, d_model]
        return self.pe[:seq_len, :]

GPT使用可学习的位置编码：

# 给出两种写法
positions_embed=nn.Embedding(max_len, d_model)
# src:[seq_len, B, d_model]
self.positional_encodings = nn.Parameter(torch.zeros(max_len, 1, d_model), requires_grad=True)

Transformer Embedding

In the embedding layers, we multiply those weights by √d_model.

class TransformerEmbedding(nn.Module):
    def __init__(self, pad_idx, vocab_size, d_model, max_len, dropout=0.1):
        super(TransformerEmbedding, self).__init__()
        self.tok_emb = nn.Embedding(vocab_size=vocab_size, d_model=d_model, padding_idx=pad_idx)
        self.pos_enc = PositionalEncoding(max_len=max_len, d_model=d_model)

        self.dropout = nn.Dropout(p=dropout)
        self.d_model = d_model

    def forward(self, x):
        '''
        enc_inputs: [batch_size, seq_len]
        '''
        # [batch_size, seq_len, d_model]
        tok_emb = self.tok_emb(x) * math.sqrt(self.d_model)

        # [seq_len, d_model]
        pos_enc = self.pos_enc(x)
        return self.dropout(tok_emb + pos_enc) # auto-broadcast

Mask

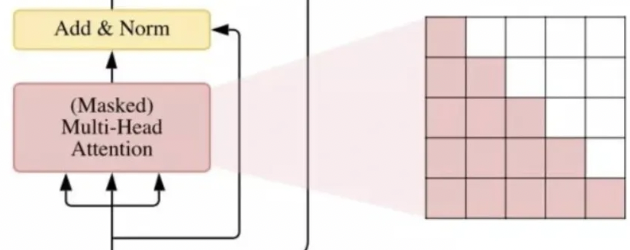
掩码操作，给不参与运算的位置赋值负无穷大，softmax 后为 0.

在 Decoder 中, dec_input_token 因为输入有先后顺序，当前位置的 token 应当只能看到它自己和左侧的 token。等同于给右侧位置的每个元素加上负无穷，要保留的位置表现为一个值为1或True的下三角矩阵。

torch.Tensor.masked_fill(mask == 0, value)
将布尔矩阵mask中值为 0 或 False 元素在 Tensor 的对应位置填充为 value。即保留了mask矩阵中值为 1 的区域。

src: pad_mask
tgt: pad_mask & sub_mask

def make_pad_mask(seq, pad_idx):
    # [batch_size, 1, 1, src_len]
    mask = (seq != pad_idx).unsqueeze(1).unsqueeze(2)
    return mask.to(seq.device)


def make_causal_mask(seq):
    batch_size, seq_len = seq.size()
    # [seq_len, seq_len]
    mask = torch.tril(torch.ones((seq_len, seq_len), device=seq.device)).bool()
    return mask


def make_tgt_mask(tgt, pad_idx):
    batch_size, tgt_len = tgt.shape
    # [batch_size, 1, 1, tgt_len]
    tgt_pad_mask = make_pad_mask(tgt, pad_idx)
    # [tgt_len, tgt_len]
    tgt_sub_mask = make_causal_mask(tgt)
    # [batch_size, 1, tgt_len, tgt_len]
    tgt_mask = tgt_pad_mask & tgt_sub_mask.unsqueeze(0).unsqueeze(0)
    return tgt_mask

Scaled Dot-Product Attention

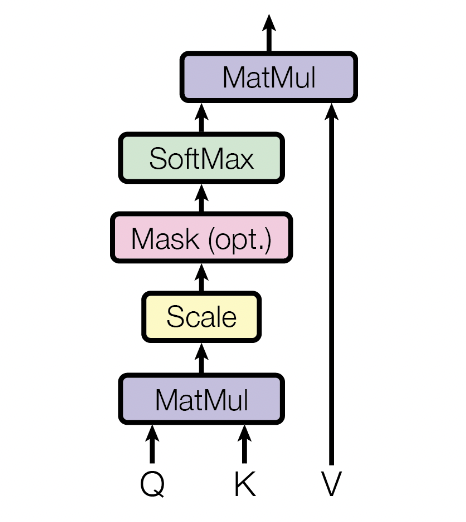
\[\text{Attention}(Q,K,V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_{key}}}\right) \cdot V\]

# Efficient implementation equivalent to the following:
def scaled_dot_product_attention(query, key, value, attn_mask=None, dropout_p=0.1) -> torch.Tensor:
    '''
    q: [batch_size, n_head, seq_len, d_k]
    
    mask: [batch_size, 1, 1, src_len]
    or [batch_size, 1, tgt_len, tgt_len]
    '''
    scale_factor = 1 / math.sqrt(query.size(-1))

    attn_weight = query @ key.transpose(-2, -1) * scale_factor
    attn_weight = attn_weight.masked_fill_(attn_mask.logical_not(), float("-inf"))
    attn_weight = torch.softmax(attn_weight, dim=-1)
    attn_weight = torch.dropout(attn_weight, dropout_p, train=True)
    return attn_weight @ value, attn_weight
    

Multi-Head Attention

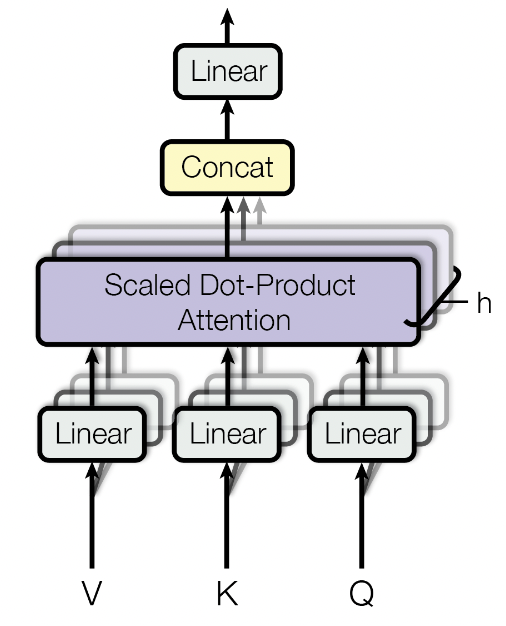
在 Encoder 的 self-attention 中，K、Q、V 均为上一层的输出经过不同线性层得到的。在 Decoder 的 cross-attention 中，K 和 V 来自 Encoder 最后一层的输出，而 Q 是 Decoder 上一层的输出。

为了使模型关注不同位置的不同特征子空间信息，我们需要使用多头注意力。具体来说，将 shape 为 [batch_size, seq_len, d_model] 的 K、Q、V 分为 [batch_size, seq_len, n_head, d_key]，再交换 seq_len 和 n_head 两个维度，以便进行 attention 机制中的矩阵乘法。计算了 attention 之后再将结果合并，并通过一个线性层映射到与输入相同的维度。算法的流程如下：

# projection
K, Q, V = W_k(x), W_q(x), W_v(x)

# split
d_key = d_model // n_head
K, Q, V = (K, Q, V).view(batch_size, seq_len, n_head, d_key).transpose(1, 2)
out = scaled_dot_product_attention(K, Q, V)

# concatenate
out = out.transpose(1, 2).view(batch_size, seq_len, d_model)
out = W_cat(out)

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, n_head, dropout=0.1):
        super(MultiHeadAttention, self).__init__()
        self.dropout = dropout
        self.n_head = n_head
        self.W_q = nn.Linear(d_model, d_model)
        self.W_k = nn.Linear(d_model, d_model)
        self.W_v = nn.Linear(d_model, d_model)
        self.W_concat = nn.Linear(d_model, d_model)
        self.attn = None

    def forward(self, q, k, v, mask=None):
        '''
        q: [batch_size, seq_len, d_model]
        mask: [[batch_size, 1, seq_len, seq_len]]
        '''
        q, k, v = self.W_q(q), self.W_k(k), self.W_v(v)

        q, k, v = self.split(q), self.split(k), self.split(v)
        
        out, attention_score = scaled_dot_product_attention(q, k, v, attn_mask=mask, dropout_p=self.dropout)
        
        self.attn = attention_score

        out = self.concat(out)
        out = self.W_concat(out)
        return out
    
    def split(self, tensor):
        '''
        [batch_size, seq_len, d_mdoel] --> [batch_size, n_head, seq_len, d_k]
        '''
        batch_size, seq_len, d_model = tensor.size()
        tensor = tensor.view(batch_size, seq_len, self.n_head, -1).transpose(1, 2)
        return tensor
    
    def concat(self, tensor):
        '''
        [batch_size, n_head, seq_len, d_k]
        '''
        batch_size, n_head, seq_len, d_tensor = tensor.size()
        d_model = n_head * d_tensor
        tensor = tensor.transpose(1, 2).contiguous().view(batch_size, seq_len, d_model)
        return tensor

Position-wise Feed-Forward Networks

FFN相当于将每个位置的Attention结果映射到一个更大维度的特征空间，然后使用ReLU引入非线性进行筛选，最后恢复回原始维度。需要说明的是，在抛弃了LSTM结构后，FFN中的ReLU成为了一个主要的能提供非线性变换的单元。

class PositionWiseFeedForward(nn.Module):
    def __init__(self, d_model, d_hidden, dropout=0.1):
        super(PositionWiseFeedForward, self).__init__()
        self.fc1 = nn.Linear(d_model, d_hidden)
        self.fc2 = nn.Linear(d_hidden, d_model)
        self.relu = nn.ReLU()
        self.dropout = nn.Dropout(p=dropout)

    def forward(self, x):
        x = self.fc1(x)
        x = self.relu(x)
        x = self.dropout(x)
        x = self.fc2(x)
        return x

LayerNorm

\(h_i = f(a_i)\) \(h'_i = f(g_i/σ_i(a_i-u_i) + b_i)\)

这样做的第一个好处（平移）是，可以让激活值落入 \(f()\) 的梯度敏感区间。梯度更新幅度变大，模型训练加快。第二个好处是，可以将每一次迭代的数据调整为相同分布（相当于“白化”），消除极端值，提升训练稳定性。

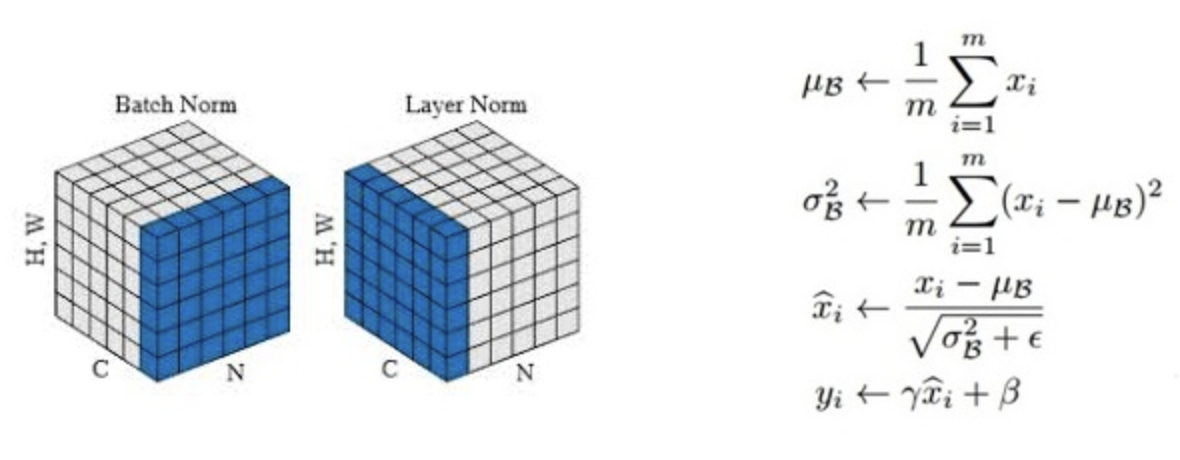
然而，在梯度敏感区内，隐层的输出接近于“线性”，模型表达能力会大幅度下降。引入 gain 因子和 bias 因子，为规范化后的分布再加入一点“个性”。需要注意的是，\(g_i\)和\(b_i\) 作为模型参数训练得到，\(u_i\)和 \(σ_i\)在限定的数据范围内统计得到。BN 和 LN 的差别就在这里，前者在某一个 Batch 内统计某特定神经元节点的输出分布（跨样本），后者在某一次迭代更新中统计同一层内的所有神经元节点的输出分布（同一样本下）。

那么，为什么要舍弃 BN 改用 LN 呢？朴素版的 BN 是为 CNN 任务提出的，需要较大的 BatchSize 来保证统计量的可靠性，并在训练阶段记录全局的 \(u\)和 \(σ\)供预测任务使用。对于天然变长的 RNN 任务，需要对每个神经元进行在每个时序的状态进行统计。这不仅把原本非常简单的 BN 流程变复杂，更导致偏长的序列位置统计量不足。相比之下，LN 的使用限制就小很多，不需要在预测中使用训练阶段的统计量，即使 BatchSize = 1 也毫无影响。

个人理解，对于 CNN 图像类任务，每个卷积核可以看做特定的特征抽取器，对其输出做统计是有理可循的；对于 RNN 序列类任务，统计特定时序每个隐层的输出，毫无道理可言——序列中的绝对位置并没有什么显著的相关性。相反，同一样本同一时序同一层内，不同神经元节点处理的是相同的输入，在它们的输出间做统计合理得多。

从上面的分析可以看出，Normalization 通常被放在非线性化函数之前。

总体的原则是在“非线性之前单独处理各个矩阵”。对于 Transformer，主要的非线性部分在 FFN（ReLU）和 Self-Attention（Softmax）的内部，已经没有了显式的循环，但这些逐个叠加的同构子层像极了 GRU 和 LSTM 等 RNN 单元。信息的流动由沿着时序变成了穿过子层，把 LN 设置在每个子层的输出位置，意义上已经不再是“落入sigmoid 的梯度敏感空间来加速训练”了，个人认为更重要的是前文提到的“白化”—— 让每个词的向量化数值更加均衡，以消除极端情况对模型的影响，获得更稳定的深层网络结构 —— 就像这些词从 Embdding 层出来时候那样，彼此只有信息的不同，没有能量的多少。在和之前的 TWWT 实验一样的配置中，删除了全部的 LN 层后模型不再收敛。LN 正如 LSTM 中的tanh，它为模型提供非线性以增强表达能力，同时将输出限制在一定范围内。因此，对于 Transformer 来说，LN 的效果已经不是“有多好“的范畴了，而是“不能没有”。

class LayerNorm(nn.Module):
    def __init__(self, normalized_shape, eps=1e-5, elementwise_affine=True):
        super(LayerNorm, self).__init__()
        self.normalized_shape = normalized_shape
        self.eps = eps
        self.elementwise_affine = elementwise_affine
        if self.elementwise_affine:
            # Learnable parameters
            self.gamma = nn.Parameter(torch.ones(normalized_shape))
            self.beta = nn.Parameter(torch.zeros(normalized_shape))
        else:
            self.gamma = None
            self.beta = None

    def forward(self, x):
        # x: [batch_size, ..., normalized_shape]
        mean = x.mean(dim=-1, keepdim=True)
        std = x.std(dim=-1, keepdim=True)
        x_normalized = (x - mean) / (std + self.eps)

        if self.elementwise_affine:
            x_normalized = self.gamma * x_normalized + self.beta

        return x_normalized

2.3 Encoder

Encoder 包含多个相同的层。上一层的输出 \(x_i\) 以如下途径经过该层：

# attention mechanism
residual = x
x = multihead_attention(q=x, k=x, v=x, mask=src_mask)
x = dropout(x)
x = layer_norm(x + residual)

# position-wise feed forward
residual = x
x = feed_forward(x)
x = dropout(x)
x = layer_norm(x + residual)

2.4 Decoder

Decoder 相较于 Encoder 除了多了一层 cross-attention 之外，还使用了 masked multi-head attention。由于模型在此处不能访问未来信息，因此这种注意力机制也称为 causal self-attention。 Decoder 同样包含多个相同的层，Encoder 最后一层的输出 enc 和 Decoder 上一层的输出 dec 以如下途径经过该层（省略了 dropout）：

# causal self-attention
residual = dec
x = multihead_attention(q=dec, k=dec, v=dec, mask=tgt_mask)
x = layer_norm(x + residual)

# cross-attention
x = multihead_attention(q=x, k=enc, v=enc, mask=src_mask)
x = layer_norm(x + residual)

# position-wise feed forward
residual = x
x = feed_forward(x)
x = layer_norm(x + residual)

2.5 Transformer

3. Training Strategy

3.1 Training Data and Batching

Attention is all you need Sec 5.1 提到，训练集使用的是 WMT 2014，每一个训练批次有大约 25k source tokens 和 25k target tokens，结果产生了 6,230 个批次。平均批次大小为 724，平均长度为 45 个 tokens。考虑到 GPU 显存不足，为了确保每个批次都有足够的 tokens，因此需要采取梯度累积策略，每 update_freq 轮才更新一次梯度。

论文还提到对 base transformer 进行了 100,000 次迭代训练，这应该对应于 16 个 epochs。

学习率更新更新这块，我理解，核心点在于大batch下的优化，bert的batch能有7w，而之所以要用大batch是因为transformer这种参数这么多的网络，少量样本太容易过拟合，必须要amount of data才能训练好参数。海量数据还用小batch训练速度实在太慢，但batch一大，会带来新问题。第一，batch大了，梯度算的准了，很容易直奔局部最优点去了，而小batch因为没那么准，有震荡，所以反而不容易陷入局部最优。第二，batch大了，同样的样本，迭代的步数就小了，而学习率在使用同样算法的情况下，基本上是不变的，加上越是底层，梯度传播过去就越大概率变小（梯度消失嘛），导致更难收敛。所以，lamd就是基于adam，学习率还考虑了当前层网络的参数，这样高层的网络更平滑，底层的网络也能加速收敛

Transformer 的学习率更新公式叫作“noam”，它将 warmup 和 decay 两个部分组合在一起，总体趋势是先增加后减小。据我所知，Transformer 是第一个使用类似设置的 NLP 模型。

第一个问题，为什么要额外设置一个 warmup 的阶段呢？虽然 NLP 中鲜有相关尝试，但是 CV 领域常常会这样做。在《Deep Residual Learning for Image Recognition》（残差网络出处）中，作者训练 110 层的超深网络时就用过类似策略：

In this case, we find that the initial learning rate of 0.1 is slightly too large to start converging. So we use 0.01 to warm up the training until the training error is below 80% (about 400 iterations), and then go back to 0.1 and continue training.

对于 Transformer 这样的大型网络，在训练初始阶段，模型尚不稳定，较大的学习率会增加收敛难度。因此，使用较小的学习率进行 warmup，等 loss 下降到一定程度后，再恢复回常规学习率。

第二个问题，为什么要用线性增加的 warmup 方式？在《Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour》有专门讨论 warmup 的小节。这篇文章将 ImageNet 上的训练时间从 Batchsize 256 in 29 hours 缩短到 Batchsize 8192 in 1 hour，而完全不损失模型精度。在解决超大 Batchsize 难优化问题时，warmup 是一个极其重要的策略。其中，线性增加的方法称为 gradual warmup，使用固定值的方法称为 constant warmup。后者的缺点是在 warmup 阶段结束时，学习率会有一次跳动抬升。

large minibatch sizes are challenged by optimization difficulties in early training and if these difficulties are addressed, the training error and its curve can match a small minibatch baseline closely.

作者认为，为了实现超大Batchsize，需要保证“k 个 minibatch , size = n , lr = η” 和 “1 个 minibatch , size = kn , lr = kη”的梯度近似相等。但是在模型变化剧烈时，这个等式会被打破。warmup 可以有效缓解这个问题。

3.2 Optimizer

3.3 Label Smoothing

Share on

Twitter Facebook LinkedIn

Celeste

Vaniila Transformer

手撕 Transformer

1. Tokenizer

2. Model details

Token Embedding

Positional Encoding

Transformer Embedding

Mask

Scaled Dot-Product Attention

Multi-Head Attention

Position-wise Feed-Forward Networks

LayerNorm

2.3 Encoder

2.4 Decoder

2.5 Transformer

3. Training Strategy

3.1 Training Data and Batching

3.2 Optimizer

3.3 Label Smoothing

Share on

You May Also Enjoy

[llms] 笔记文档

一、简介

1. 需求和技术

2. 整体步骤说明

3. 模型微调

4. 模型部署和暴露接口

5. web后端调用

[llms] Docs

个人向学习文档

采样

sample

MoE 原理及实现

MoE：mix of experts